Виды средних величин и способы их вычисления

В статистике применяются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, а также структурные средние – мода, медиана и др.

Наиболее распространенным видом средних величин в статистике является средняя арифметическая, представляющая собой частное от деления суммы индивидуальных значений признаков на их количество.

Средняя арифметическая величина бывает простой и взвешенной.

Допустим, что количество правонарушений по 10 населенным пунктам региона за отчетный период составило: 3100, 3600, 4500, 4900, 5300, 5400, 5600, 5700, 5900, 6000. Состояние преступности одного населенного пункта само по себе не может дать представление об ее уровне по всему региону. Для этого надо определить средний уровень преступности. Его в данном примере можно определить так: суммируем состояние преступности по всем населенным пунктам и полученный итог разделим на число населенных пунктов в обследуемом регионе. Это составит следующее количество преступлений:

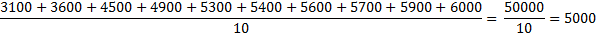
Среднегодовой уровень преступности по региону составляет 5000 преступлений. Это простая средняя арифметическая величина.

Простой она называется потому, что исчисляется простым суммированием индивидуальных значений признака и делением этой суммы на число значений.

Отдельные значения признака единицы статистической совокупности, отличные от значений его у других единиц (в нашем примере уровень преступности по каждому населенному пункту – 400, 3600, 4500 и т.д.), в статистике принято называть вариантами и обозначать символом х_i где i может принимать любые значения от 1 до n. При наличии в совокупности n вариантов последний из них обозначается х_n. В нашем примере n = 10, таким образом, х₁ = 3100, х₂ = 3600, ..., x₁₀ = 6000. Величина среднего варианта обозначается 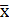, а знак суммы вариантов — через .

Расчет средней арифметической простой можно записать в виде следующей формулы:

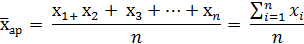
Средняя величина исчисляется по формуле средней арифметической простой тогда, когда значения вариантов встречаются по одному или по одинаковому числу раз, т.е. когда повторяемость каждого варианта одинакова.

Если же отдельные значения признака повторяются неодинаковое число раз, то средняя величина определяется по формуле средней арифметической взвешенной. Для примера возьмем данные о состоянии преступности в различных населенных пунктах, представленные в табл. 6.1.

Таблица 6.1