Членов преступных групп
| Количество членов группы, чел. | ||||||||
| Количество уголовных дел |
Модальной величиной в данном случае будет преступная группа, в составе которой 4 человека, так как этому значению в нашем ряду распределения соответствует наибольшее количество уголовных дел – 260.
В отличие от дискретных вариационных рядов вычисление моды в интервальных рядах осуществляют по следующей формуле:
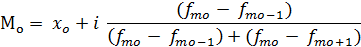
где 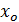 – нижняя граница модального интервала (модальным является интервал, имеющий наибольшую частоту);
– нижняя граница модального интервала (модальным является интервал, имеющий наибольшую частоту);
i – величина модального интервала;
fmo – частота модального интервала;
fmo-1 – частота интервала, предшествующего модальному;
fmo+1 – частота интервала, следующего за модальным.
Медианой (Ме), или серединным значением наблюдаемой совокупности, в статистике называют величину варьирующего признака, которая находится в середине ряда, расположенного в порядке возрастания или убывания. Иначе можно сказать, что медиана – это серединное значение ранжированного вариационного ряда.
Для определения места медианы в дискретном вариационном ряду надо к сумме частот этого ряда пприбавить единицу и полученное число разделить на 2:
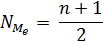
где 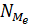 – место медианы;
– место медианы;
n – объем совокупности (сумма частот).
Например, в одном городском суде по уголовным делам было осуждено в течение месяца 11 человек со следующими сроками лишения свободы:
| № осужденного | ||||||||||
| Срок лишения свободы, лет | ||||||||||
| 1,5 | 2,5 | 3,5 |
В нашем примере номер медианы равен 6, а медиана равна 3 годам, т.е. одна половина осужденных к лишению свободы получила срок наказания менее 3 лет, а другая – более 3 лет лишения свободы.
Если ряд имеет четное число индивидуальных значений (вариантов), то медиана равна средней из двух вариантов, находящихся в середине ряда.
| № осужденного | |||||||||
| Срок лишения свободы, лет | |||||||||
| 1,5 | 2,5 | 3,5 |
В этом случае 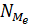 = 5,5, а медиана равна средней арифметической двух соседних значений 2,5 и 3, т.е. Me = 2,75 года.
= 5,5, а медиана равна средней арифметической двух соседних значений 2,5 и 3, т.е. Me = 2,75 года.
Дата добавления: 2017-05-18; просмотров: 477;
