Показатели размера вариации
Для характеристики величины возможных колебаний наблюдаемых единиц совокупности в статистике исчисляют следующие показатели размера вариации: размах вариации, среднее линейное отклонение, средний квадрат отклонения (дисперсия), среднее квадратическое отклонение и коэффициент вариации (рис. 6.2).
Наиболее простым измерителем вариации является размах вариации, представляющий собой разность между наибольшим и наименьшим значениями варьирующего признака:
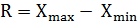
где 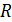 – размах вариации;
– размах вариации;
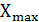 – наибольшее значение признака;
– наибольшее значение признака;
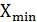 – наименьшее значение признака.
– наименьшее значение признака.
Размах вариации имеет теоретическое и практическое значение: с его помощью определяют допустимые размеры колебаний, сравнивают их с установленными границами.
Главный недостаток размаха вариации заключается в том, что он не отражает существенные черты варьирования признака. Таким образом, размах вариации не может служить основным показателем меры вариации наблюдаемого признака.
Более точную характеристику вариации признака можно получить, если сравнить все имеющиеся значения с их средней величиной.
В этом случае будет исчислен другой показатель колебаний изучаемого признака – среднее линейное отклонение (d), которое представляет собой среднюю арифметическую величину из абсолютных значений отклонений вариант признака от их среднего значения.
Среднее линейное отклонение может быть простым и взвешенным.
Формула простого среднего линейного отклонения имеет следующий вид:
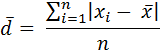
где 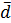 – среднее линейное отклонение;
– среднее линейное отклонение;
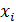 – конкретное значение признака;
– конкретное значение признака;
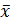 – среднее значение признака;
– среднее значение признака;
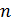 – число вариантов.
– число вариантов.
Взвешенное значение среднего линейного отклонения определяют по формуле:
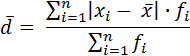
где 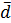 – среднее линейное отклонение;
– среднее линейное отклонение;
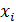 – конкретное значение признака;
– конкретное значение признака;
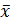 – среднее значение признака;
– среднее значение признака;
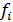 – частота повторений.
– частота повторений.
Среднее линейное отклонение, так же как и размах вариации, нельзя считать достаточно точным показателем, не говоря уже о гом, что он вообще теряет всякий смысл, если учитывать знаки отклонений вариант от средней арифметической величины. Чтобы преодолеть недостатки среднего линейного отклонения, вычисляют средний квадрат отклонений, или дисперсию.
Средний квадрат отклонения, или дисперсия, представляет собой среднеарифметическую величину из квадратов отклонений вариант от их средней арифметической и обозначается символом 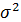 . Формула простого (невзвешенного) квадрата отклонения (невзвешенной дисперсии) имеет вид:
. Формула простого (невзвешенного) квадрата отклонения (невзвешенной дисперсии) имеет вид:
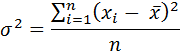
Взвешенное значение квадрата отклонения (взвешенной дисперсии) вычисляется по формуле:
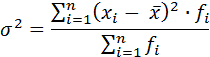
При возведении отклонений вариант от средней арифметической величины в квадрат положительные и отрицательные отклонения получают один и тот же положительный знак. Кроме того, большие отклонения от средней величины, будучи возведенными в квадрат, получают и больший «удельный вес», оказывая большее влияние на величину показателя вариации. Однако, возводя отклонения вариант от средней арифметической величины в квадрат, мы искусственно увеличиваем и сам показатель вариации.
Чтобы преодолеть этот недостаток, вычисляется среднее квадратическое отклонение ( 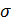 ), которое исчисляется путем извлечения квадратного корня из среднего квадрата отклонения (дисперсии). Простое (невзвешенное) среднее квадратическое отклонение определяется по формуле:
), которое исчисляется путем извлечения квадратного корня из среднего квадрата отклонения (дисперсии). Простое (невзвешенное) среднее квадратическое отклонение определяется по формуле:
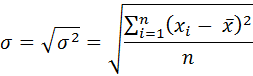
Формула для определения взвешенного среднего квадратического отклонения имеет вид:
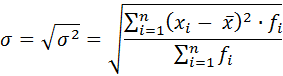
Для сравнения колебаний разнородных явлений, разных по своему характеру и размерам признаков, используется относительный показатель вариации, так называемый коэффициент вариации. Коэффициент вариации дает возможность сопоставить вариацию одного и того же признака в разных статистических совокупностях, а также разнородных признаков одной и той же или различных статистических совокупностей. Коэффициент вариации обозначается буквой V.
Наиболее часто в практических целях применяют коэффициент вариации, который представляет собой процентное отношение средней квадратической ошибки к средней арифметической величине:
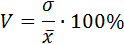
Иногда применяется линейный коэффициент вариации, который определяют как процентное отношение среднего линейного отклонения к средней арифметической величине:
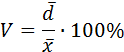
Коэффициент вариации как относительный показатель может быть представлен в коэффициентном или в процентном выражении.
Дата добавления: 2017-05-18; просмотров: 3067;
