Ведомость вычисления координат точек теодолитного хода
| Названия точек | Измеренные углы | Дирекционные углы | Длины сторон, м | Приращения координат, м | Координаты, м | |||
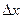
| 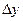
| x | y | |||||
| A | ||||||||
| -0,3¢ | 349º 50,0′ | |||||||
| I | 113º 26,0′ | -0,03 | +0,04 | 6322,70 | 4057,25 | |||
| -0,3 | 56 24,3 | 138,56 | +76,67 | +115,42 | ||||
| II | 85 07,5 | -0,03 | +0,03 | 6399,34 | 4172,71 | |||
| -0,3 | 151 17,1 | 116,30 | -102,00 | +55,88 | ||||
| III | 211 44,5 | -0,04 | +0,05 | 6297,31 | 4228,62 | |||
| -0,3 | 119 32,9 | 197,24 | -97,27 | +171,59 | ||||
| IV | 56 33,2 | 6200,00 | 4400,26 | |||||
| 243 00,0 | ||||||||
| B | ||||||||
| Sb = 466°51,2′ | P = Sd = 452,10 | SDx = = -122,60 | SDy = = +342,89 | |||||
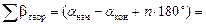
| 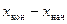 = -122,70; = -122,70; 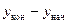 = 343,01; = 343,01;
| |||||||
= 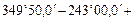 4×180° - 4×180° -
| 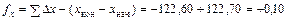 м м
| |||||||
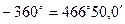
| 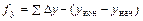 = + 342,89 - 343,01 = - 0,12 м = + 342,89 - 343,01 = - 0,12 м
| |||||||
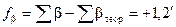
| 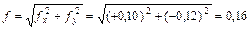 м м
| |||||||
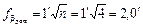
| 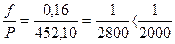
| |||||||
Вычисленную угловую невязку сравнивают с допустимой
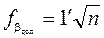 .
.
Если угловая невязка меньше допустимой, что указывает на доброкачественность угловых измерений и правильность вычислений, то невязку 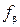 распределяют поровну во все измеренные углы со знаком, противоположным знаку невязки. Полученные при этом поправки
распределяют поровну во все измеренные углы со знаком, противоположным знаку невязки. Полученные при этом поправки
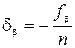
вписывают над измеренными углами в графу 2. Невязка редко делится на число углов без остатка. Поэтому поправки округляют, вводя бо¢льшие в углы с более короткими сторонами. При этом сумма поправок должна равняться невязке с обратным знаком: Sdb = -fb.
Вычисление дирекционных углов. Дирекционные углы вычисляют, используя начальный дирекционный угол 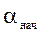 и измеренные углы bi, исправленные поправками db, по формулам:
и измеренные углы bi, исправленные поправками db, по формулам:
для правых углов - 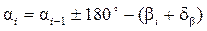 ;
;
для левых углов - 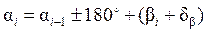 .
.
Здесь индексы i = 1, 2, …, n соответствуют номерам углов и сторон на рис. 6.5 а, причем a0 = aнач и an = aкон.
Контролем правильности вычислений служит равенство вычисленного и заданного значений конечного дирекционного угла.
Вычисление приращений координат выполняют по дирекционным углам и длинам сторон хода (графы 5 и 6).
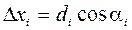 ;
; 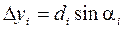 (i = 1, 2, …, n-1).
(i = 1, 2, …, n-1).
Вычислив суммы приращения абсцисс 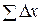 и ординат
и ординат 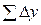 , находят координатные невязки
, находят координатные невязки
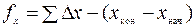 ,
, 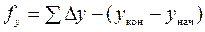 . (6.3)
. (6.3)
Вычисляют абсолютную невязку 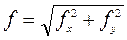 и относительную невязку хода f / P,где
и относительную невязку хода f / P,где 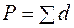 - длина хода. Если относительная невязка не превосходит допустимой (обычно, 1/2000), то невязки fx и fy распределяют (см. записи курсивом в графах 5 и 6), в виде поправок к приращениям координат,пропорциональных длинам сторон, и со знаками, противоположными знакам невязок:
- длина хода. Если относительная невязка не превосходит допустимой (обычно, 1/2000), то невязки fx и fy распределяют (см. записи курсивом в графах 5 и 6), в виде поправок к приращениям координат,пропорциональных длинам сторон, и со знаками, противоположными знакам невязок:
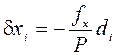 ;
; 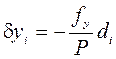 . (6.4)
. (6.4)
Суммы поправок должны равняться невязкам с обратным знаком:
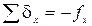 ;
; 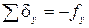 .
.
Если из-за выполненных округлений равенства нарушаются, поправки, вычисленные по формулам (6.4), несколько изменяют, добиваясь соблюдения равенств.
Вычисление координатточек теодолитного хода выполняют по формулам (см. графы 7 и 8)
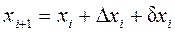 ;
; 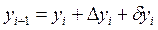 (i = 1, 2, …, n-1).
(i = 1, 2, …, n-1).
Контролем правильности вычислений служит совпадение вычисленных и заданных координат последней точки теодолитного хода.
Обработка замкнутого теодолитного хода.
Последовательность обработки замкнутого хода такая же как и разомкнутого. Но исходными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. Это накладывает на обработку замкнутого хода следующие особенности.
Угловая невязка вычисляется по формуле (6.2), в которой в отличие от разомкнутого хода
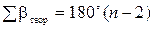 ,
,
где n – число углов в полигоне.
После распределения угловой невязки и вычисления дирекционных углов сторон хода контролируют правильность вычислений - в конце должно быть получено то же значение дирекционного угла, которое было исходным.
Невязки в координатах находят по формулам:
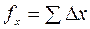 ,
, 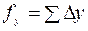 .
.
Эти соотношения следуют из формул (6.3), где в данном случае 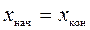 ,
, 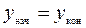 . Распределив невязки fx и fy и вычислив координаты точек хода, контролируют правильность вычислений - вычисленные в конце координаты начальной точки хода должны равняться исходным.
. Распределив невязки fx и fy и вычислив координаты точек хода, контролируют правильность вычислений - вычисленные в конце координаты начальной точки хода должны равняться исходным.
Дата добавления: 2019-04-03; просмотров: 808;
