Частные производные высших порядков

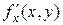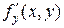Если функция f(x, y) определена в некоторой области D, то ее частные производные и тоже будут определены в той же области или ее части. Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второгопорядка: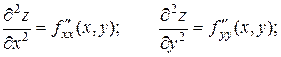

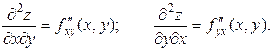
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков. Частные производные вида 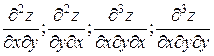и т.д. называются смешанными производными.

Теорема (Шварц). Двесмешанные частные производные одного порядка одной и той же функции, отличающиеся лишь порядком дифференцирования, в случае, когда они являются непрерывными функциями, равны между собой (например ).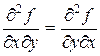

Т.е. частные производные высших порядков не зависят от порядка дифференцирования.

Пример 14.Найти все частные производные второго порядка функции .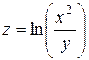

Решение.Используя свойства логарифмов преобразуем выражение 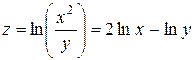. Найдем частные производные первого порядка 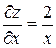и 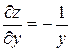. Найдем частные производные второго порядка 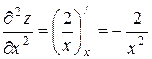, , 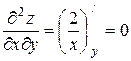, 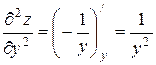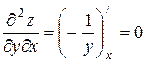.[10]