Предел и непрерывность функции двух переменных

Число А называется пределом функции f(x, y) при стремлении точки М(х,у) к точке М₀(х₀, у₀), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие 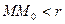, также верно и условие .

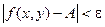Записывают: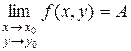

Пример 2. Вычислить пределы:

а) .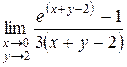

Решение. .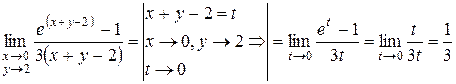

б) .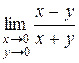

Решение. Функция 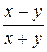определена в проколотой окрестности точки О(0; 0) вне прямой 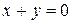; поэтому условие 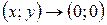означает, что .

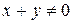Если здесь применять обычный метод «проб и ошибок», то можно получить следующие результаты:

1) устремим М(x; y)к О(0; 0) вдоль оси Ох, т.е. примем у=0, а 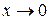, то ;

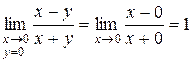2) устремим М(x; y)к О(0; 0) вдоль оси Оу, т.е. примем х=0, а 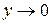, то .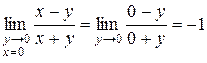

Разные предельные значения означают, что данный предел не существует.

3) .

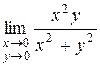Решение.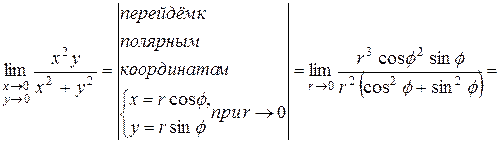

.

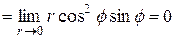Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀,у₀), если 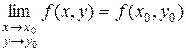(1); причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом.

Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрывафункции f(x, y). Это может быть в следующих случаях:

1) Функция z = f(x, y) не определена в точке М₀(х₀, у₀).

2) Не существует предел .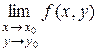

3) Этот предел существует, но он не равен f(x₀, y₀).

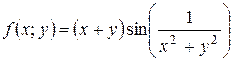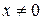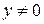Пример 3. Непрерывна ли функция при , и .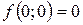

Решение.Проверим условия непрерывности функции в точке О(0; 0):

1) Функция f(x, y) определена в окрестности этой точки.

2) 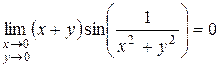, так как имеем 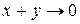, а 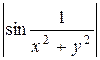ограничена.

3) Предел в точке равен значению функции в этой точке 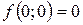. Функция непрерывна в точке О (0; 0).

Функция непрерывна в каждой точке 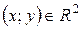как комбинация непрерывных элементарных функций.