Полное приращение и полный дифференциал функций нескольких переменных
Для функции f(x, y) выражение Dz= f(x+Dx,y+Dy)–f(x, y) называется полным приращением.
Если функция f(x, y) имеет непрерывные частные производные, то
.
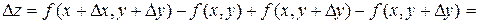
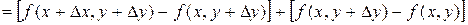Применив теорему Лагранжа[7] к выражениям, стоящим в квадратных скобках, получаем:
, 
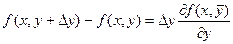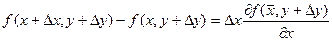, здесь 
. Следовательно 
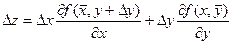. Т.к. частные производные непрерывны, то можно записать равенства: 
, 
.
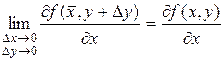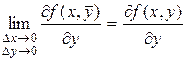Выражение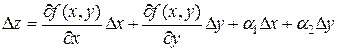 
называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх®0 и Dу® 0 соответственно.
Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у):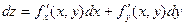 
.
Для функции произвольного числа переменных:
Пример 7. Найти полный дифференциал функции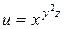 
.
Решение.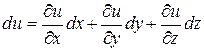 
(1)
Найдем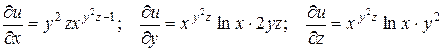 
, подставим в формулу (1), получим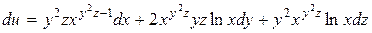 
Пример 8. Найти полный дифференциал функции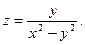 
Решение.Найдем частные производные и подставим в формулу:
, 
.
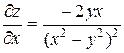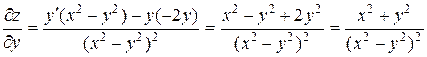
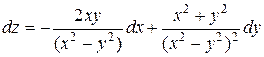Геометрический смысл полного дифференциала[8]
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Дата добавления: 2017-12-05; просмотров: 1916;