Теорема (достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение: 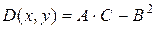, где , , .

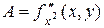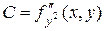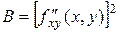1) Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если 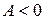- максимум, если 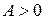- минимум.

2) Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума.

3) Если D = 0, вывод о наличии экстремума сделать нельзя, необходимы дополнительные исследования.

Пример 19. Найти точки экстремума функции .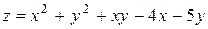

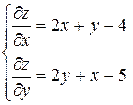
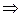
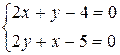
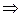
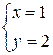
Решение. Находим частные производные первого порядка 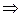М(1; 2) – критическая точка.

Найдём значения вторых производных в точке М(1; 2):

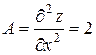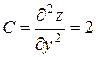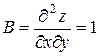, , .Тогда 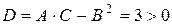. Так как 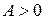, то в точке М(1; 2) функция имеет минимум .

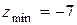Пример 20.Исследовать на экстремум функцию 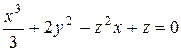, заданную неявно.

Решение. Схема исследований та же, только все параметры задачи надо определить по методам функций, заданных неявно.

1. Найдём критические точки.

Пусть 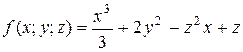, тогда

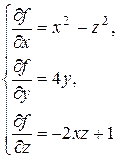
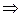
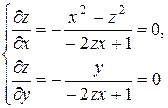
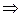
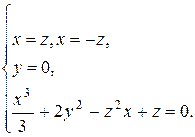
В третьей системе присоединяем данное уравнение. Решением системы являются точки 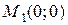, , 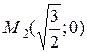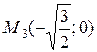. Если 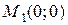, то 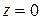, 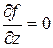следовательно, уравнение в этой точке не определяет однозначную функцию и эта точка не подлежит исследованию.

2. Для проверки достаточных условий найдём вторые частные производные по правилам дифференцирования неявных функций:

, , .

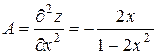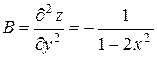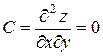При 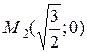: 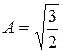, , 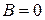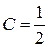. 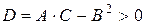, т.к.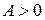 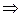в точке 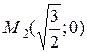- минимум.

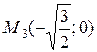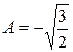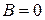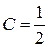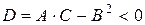
При : , , . 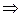в точке 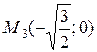- экстремума нет.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, т.е. существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи. Отыскание условного экстремума можно свести к исследованию на обычный экстремум так называемой функцией Лагранжа[11] u = f(x, y) + lj(x,y), где l - неопределённый постоянный множитель. Необходимые условия экстремума функции Лагранжа имеют вид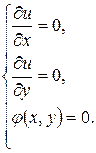

Замечание. Если вторые частные производные не содержат 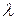, то процесс нахождения условного экстремума вырождается в процесс нахождения локального (абсолютного) экстремума функции 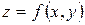− что не приемлемо. Тогда для исследования на экстремум в полученных критических точках вычисляем значение .

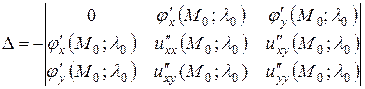Если 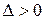, то функция 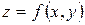в точке 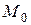имеет условный минимум; если 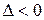- то условный максимум.

Пример 21. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0.

Решение.Составим функцию Лагранжа .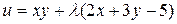

Найдем частные производные и составляем необходимые условия экстремума для функции Лагранжа: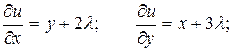

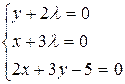
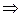
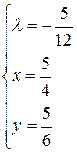
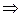М₀ 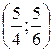- стационарная точка. Для исследования на экстремум в полученных критических точках вычисляем значения 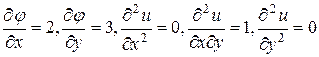и составляем определитель 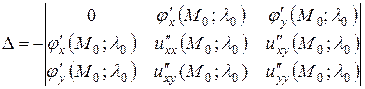= 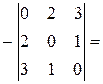-12.

Т.к 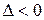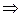в точке М₀ 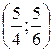функция f(x, y) = xy имеет условный максимум.

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.