I. Неопределенный интеграл.

Первообразная функции.

Пусть функция 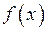определена на некотором интервале 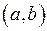. Тогда функция 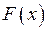называется первообразной для функции 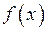на интервале 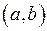, если

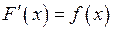
для всех .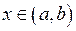

I. Неопределенный интеграл.

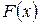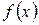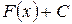Теорема 1. Если – первообразная для функции , то , где 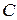– любое число, также первообразная для функции .

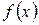Теорема 2. Есл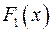и и 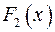– первообразные для функции 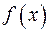, на промежутке 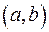, то разность 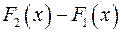есть постоянная величина.

Из теорем 1 и 2 следует, что если для функции 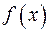существует какая-нибудь первообразная 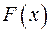, то для 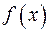существует бесконечное множество первообразных отличающихся друг от друга на постоянное слагаемое.

Теорема 3. Если 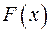– первообразная для функци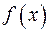и и 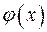– функция, у которой существует 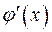, то 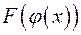– первообразная для .

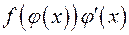Определение. Неопределенным интегралом от функции 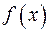называется сумма какой-либо первообразной для этой функции и произвольной постоянной.

Из теоремы 1 о первообразной функции следует, что неопределенный интеграл от функции 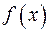есть множество всех первообразных для этой функции. Обозначени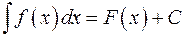е: , где 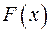– некоторая первообразная для 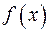, 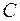– произвольная постоянная, 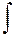– означает неопределенный интеграл, 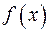называется подынтегральной функцией, 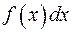– подынтегральным выражением, 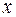– переменной интегрирования.