Производная от функции, заданной параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений: 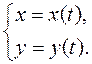, где t – вспомогательная переменная, называемая параметром. Имеем обратную функцию 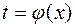. Считая, что функции дифференцируемы, получаем: 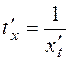, а по правилу дифференцирования сложной функции имеем: . .

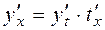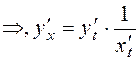Пример 10.Пусть 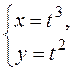. Найти .

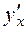Решение. .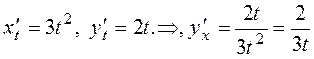

Дифференциал функции и его геометрический смысл

Пусть функция y = f(x) имеет производную в точке х: 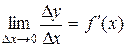. Тогда можно записать: 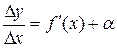, где a®0, при Dх®0. Следовательно: 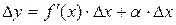. Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.

Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции. Обозначается dy или df(x).

Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.

Геометрический смысл дифференциала

Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx. Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в этой точке, когда x получит приращение Dx (Рис. 12).

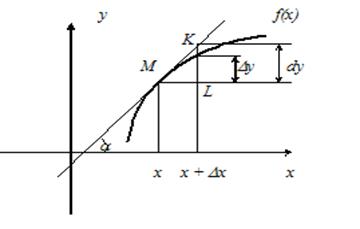
Рис. 12