Непараметрические методы оценивания
| Всякая научная область жизнеспособна, пока в ней избыток новых проблем. Д. Гильберт. Доклад на втором Международном конгрессе математиков. Может ли быть тот или другой предмет, то или другое явление реального мира исследуемо с помощью данного математического метода – это вопрос решается не конкретной материальной природой предмета или явления, но исключительно их формальными структурными свойствами и прежде всего теми количественными соотношениями и пространственными формами, в которых они живут или протекают. Гнеденко Б.В. "Математика и научное познание". |
Непараметрические методы применяют тогда, когда закон распределения исследуемого показателя неизвестен и нет необходимости его аналитического описания. Эти методы проще в реализации, чем параметрические, но они не позволяют осуществлять прогноз значений показателей надежности. К непараметрическим относят методы последовательного перехода к новой системе координат, построения "множительной" оценки, ядерных оценок, будстрепа и другие. С прикладной точки зрения методы различаются сложностью реализации и качеством получаемых оценок. Однако характеристики качества получаемых оценок исследованы не для всех методов, особенно слабо проработаны эти вопросы применительно к малым объемам выборок.
Далее, не нарушая общности выводов и положений, для конкретности будем рассматривать вопросы оценки показателей безотказности (аналогичные подходы справедливы и для других показателей). Построение эмпирической функции распределения наработки до отказа по формуле FN(t)=i/N при t>0 (где N – объем выборки; i – количество наработок до отказа, попавших в интервал [0, t ], i=1, 2, ..., N) применимо для планов [NUr], [NUТ] и [NUz] в области полных наработок, но недопустимо в целом ко всей цензурированной выборке (так как этот подход предполагает использование информации по всей выборке). Если исключить все неполные наработки (наработки до цензурирования), то будут иметь место значительные ошибки в определении оценки FN(t). Наличие цензурирования приводит к неопределенности для FN(t) в области цензурирования, которая увеличивается с ростом числа неполных наработок.
Постановка задачи определения показателей надежности по цензурированным выборкам формулируется следующим образом.
Имеются выборочные значения наработки до отказа
t1 , t2 , …, tr
и до цензурирования
t1, t2, ..., tk.
Количество наработок до отказа r и до цензурирования k, объем выборки N=r+k.
Необходимо определить: эмпирическую функцию распределения наработок до отказа, оценку вероятности безотказной работы, среднее значение (оценку математического ожидания) наработки до отказа.
Допущения: результаты получены с использованием одного из планов типа [NUr], [NUТ] или [NUz].
Решение задачи включает выполнение следующих этапов:
предварительная обработка ЭД;
построение эмпирической функции распределения FN(t);
определение оценки вероятности безотказной работы p*(t) и средней наработки до отказа Тo.
Предварительная обработка ЭД предусматривает построение общего вариационного ряда, для этого наработки на отказ и на цензурирование упорядочивают в порядке неубывания. Если отдельные наработки до отказа равны наработкам до цензурирования, то в вариационном ряду первыми ставятся наработки до отказа.
К числу основных методов построения эмпирической функции распределения относятся методы последовательного перехода к новой системе координат и множительной оценки.
Рассмотрим метод последовательного перехода к новой системе координат. Период времени наблюдения разбивается на m непересекающихся интервалов, границы которых совпадают со значениями наработок до цензурирования, возможно за исключением крайних интервалов. Если вариационный ряд начинается с наработки до отказа, то k0=0 и первый интервал определяется границами [0, t1], иначе k0 равно числу неполных наработок, с которых начинается ряд, и первый интервал соответствует границам [tl, tl+1], где l=k0. Если вариационный ряд заканчивается наработкой до отказа, то km=0 и правая граница последнего интервала равна наработке до отказа tr, иначе последний интервал имеет открытую правую границу (правая граница соответствует бесконечности). Для каждого интервала наблюдения подсчитывается число наработок до отказа и число наработок до цензурирования ki. Например, общий вариационный ряд
t1, t2, t3, t1, t4, t2, t3, t5
разбивается на интервалы наблюдений
[0, t1], [t1, t2], [t2, t3], [t3, t5],
а значения ri и ki для указанных интервалов будут равны
(3,1), (1,1), (0,1), (1,0)
соответственно. Когда вариационный ряд заканчивается наработкой до отказа, то
FN(tm)=1,
иначе
FN(tm)<1.
Количество объектов Nu,i, за которыми ведется наблюдение на i-м интервале [ti–1, ti], определяется из соотношений:
Nu,1=N–k0, 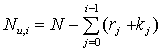 , r0=0. , r0=0.
| ( 8 .1) |
Такая выборка рассматривается как полная выборка для интервала [ti–1, ti], она цензурирована слева граничным временем ti этого интервала. Эмпирическая функция распределения на текущем интервале строится по полной выборке объема Nu,i в новой системе координат при постоянном масштабе по оси времени, а по оси вероятностей – с масштабным коэффициентом 1–FN(ti–1). Каждый интервал характеризуется эквивалентным объемом
Nэ,1=N–k0,
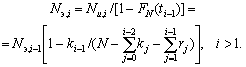
| (8.2) |
Изделия, находящиеся под наблюдением в очередном интервале времени, имеют одинаковую вероятность отказа. Величина, обратная эквивалентному объему, соответствует приращению функции распределения за одну наработку в текущем интервале наблюдения, т.е. внутри каждого интервала приращение функции распределения по одной наработке до отказа составляет 1/Nэ,i. Тогда для n-й наработки до отказа (n – номер элемента общего вариационного ряда), соответствующей интервалу наблюдения i,
FN(tn) = (n–k0)/Nэ=1, для i=1;
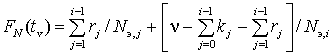 , для i=2, 3, ..., m. , для i=2, 3, ..., m.
| (8.3) |
Пример 8.1.Проведено испытание десяти объектов по плану [NUz]. Наработки шести объектов до отказа составили 1922, 2576, 2314, 1873, 2135, 2018 часов. К моменту оценки четыре объекта безотказно проработали 2107, 3936, 2010, 2397 часов. Необходимо построить эмпирическую функцию распределения наработки до отказа.
Решение. Построим общий вариационный табл. 8.1 (звездочками помечены наработки на цензурирование).
Таблица 8.1
| n | ||||||||||
| tn | 2010 * | 2107 * | 2397 * | 3936 * | ||||||
| tr | t1 | t2 | t3 | t4 | t5 | t6 | ||||
| tk | t1 | t2 | t3 | t4 | ||||||
| i | ||||||||||
| ri | ||||||||||
| ki |
Вариационный ряд начинается с наработки на отказ, следовательно, r0=0. Количество объектов наблюдения Nu,i по интервалам:
Nu,1=10 – 0=10; Nu,2 = 10 – (2+1) = 7;
Nu,3 = 10 – (2+1+1+1) = 5; Nu,4 = 10 – (2+1+1+1+2+1) = 2.
Эквивалентные объемы выборок для интервалов наблюдения:
Nэ,1 = 10 – 0 = 10; Nэ,2 = 10[1 – 1/(10 – 0 – 2)] =10[1 – 1/8] = 8,75;
Nэ,3 = 8,75[1 – 1/(10 – 1 – (2 + 1))] = 8,75[1 – 1/6] = 7,29;
Nэ,4 = 7,29[1 – 1/(10 – (1+1) – (2+1+2))] = 7,29[1 – 1/3] = 4,86.
Эмпирическая функция распределения наработок до отказа:
F10(t1) = (1 – 0)/10 = 0,1; F10(t2) = (2 – 0)/10 = 0,2;
F10(t4) = 2/10 + [4 – 1 – 2]/8,75 = 0,2 + 1/8,75 = 0,314;
F10(t6) = (2/10+1/8,75) + [6–2–3]/7,29 = 0,314+1/7,29 =0,451;
F10(t7) = 0,314 + [7 – 2 – 3] /7,29 = 0,589;
F10(t9) = (0,314 + 2/7,29) + [9 – 3 – 5]/4,86 = 0,794.
В методе множительной оценки определение оценки вероятности безотказной работы и эмпирической функции распределения наработки до отказа производится по простым соотношениям
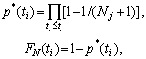
| (8.4) |
где Nj – количество работоспособных объектов после отказа при наработке ti. По эмпирической функции распределения наработки до отказа или по функции вероятности безотказной работы можно получить оценки других показателей надежности невосстанавливаемых изделий. Точечная оценка вероятности безотказной работы за наработку t (t<tn) определяется с помощью линейной интерполяции значений эмпирической функции вероятности безотказной работы по формуле
p*(t) =dp*(tv) + (1–d) p*(tv-1)],
где tv–1 и tv – наработки до отказа, между которыми лежит наработка t,
d=(t – tv–1)/(tv – tv-1).
При известном законе распределения средняя наработка до отказа определяется из соотношения
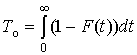 .
.
Для цензурированных слева выборок время наблюдения ограничено, что позволяет получить только нижнюю границу средней наработки до отказа путем замены интеграла соответствующей суммой, верхнего предела – временем наблюдения, а функции распределения – ее оценкой:
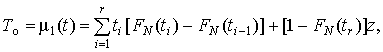
| (8.5) |
где z = max (tr, tk); t0=0.
Эмпирическую плотность распределения наработки до отказа при достаточно малом интервале Dti=ti–ti–1 можно представить в виде
fN(ti–1, ti) = [FN(ti) – FN(ti–1)]/Dti.
Точность такого представления зависит от длины интервала, его положения на оси наработок. В целях повышения точности представления fN(ti–1, ti) рекомендуется проводить ее сглаживание, например, используя ядерные оценки, которые дают хороший эффект при малом числе отказов на интервале.
Интенсивность отказов полностью определяется законом распределения. Для многократно цензурированных выборок оценка интенсивности отказов
l*(ti – ti– 1) = ri / [Nu,i (ti – ti–1)] при Nu,i > 0.
Дисперсия оценки интенсивности возрастает с ростом функции распределения.
Основные свойства оценок рассмотренных параметров определяются свойствами функции распределения наработки до отказа, в частности, если оценка функции несмещенная, то и оценка нижней границы средней наработки до отказа также будет несмещенной. Предложенная оценка функции распределения применима для выборок, многократно и однократно цензурированных слева.
Эта же оценка применима и к функции распределения выборок, цензурированных справа или интервалом. Простым переходом к такому применению является приравнивание начала неопределенных на периоде наблюдения наработок до отказа (начало таких наработок лежит вне периода наблюдения и поэтому точно неизвестно) некоторой правдоподобной величине, например, правой границе или середине интервала неопределенности. Однако точность такой аппроксимации функции распределения весьма невелика.
Пример 8.2.Используя метод множительных оценок для условий примера 8.1, построить эмпирическую функцию распределения наработки до отказа, оценить среднюю наработку до отказа и вероятность безотказной работы за наработку 2000 часов.
Решение. Воспользуемся методом множительной оценки вероятностей безотказной работы и эмпирической функции распределения наработки до отказа:
| p*(t <1873)=1; p*(t1) = p*(1873) = 1– 1/10=0,9; p*(t2) = p*(1922) = 0,9(1–1/9)=0,8; p*(t4) = p*(2018) = 0,8(1–1/7)=0,686; p*(t6) = p*(2135) = 0,686(1 – 1/5)=0,549; p*(t7) = p*(2314) = 0,549(1 – 1/4)=0,411; p*(t9) = p*(2576) = 0,397(1 – 1/2)=0,206; | F10(t <1873)=0; F10(t1) = 1– p*(1873) = 0,1; F10(t2) = 0,2; F10(t4) = 0,314; F10(t6) = 0,451; F10(t7) = 0,589; F10(t9) = 0,794. |
Как видно, оценки значений функции распределения полностью совпали с оценками, рассчитанными по методу перехода к новой системе координат. Оценка средней наработки до отказа
То = m1(t)=1873(0,1 – 0)+1922(0,2 – 0,1)+2018(0,314 – 0,2)+
+2135(0,451 – 0,314)++2314(0,589 – 0,451)+
+2576(0,794 – 0,589)+(1 – 0,794)3936 = 2559,9 ч.
Простое вычисление среднего значения по всем наработкам дает величину, равную 2328,8 ч, что меньше То.
Оценка вероятности безотказной работы за наработку 2000 ч:
d = (2000 – 1922)/(2018 – 1922)=0,813;
p*(2000)=(0,813) (0,686)+(1– 0,813)0,8=0,707.
Рассмотренные подходы к построению эмпирической функции распределения просты в реализации, не требуют большого объема данных и сложных вычислений. Они позволяют получить (за исключением ряда ситуаций, в которых Nu,i=0) несмещенные, состоятельные, асимптотически нормальные оценки значений функции распределения наработки изделия до отказа. Существенным недостатком оценок является невозможность их применения в интересах прогнозирования надежности исследуемых изделий. Преодоление данного недостатка возможно на основе параметрического оценивания показателей, которое позволяет получать оценки с более высокой точностью, чем непараметрические методы.
Дата добавления: 2017-10-09; просмотров: 1418;
