Дифференциальное исчисление функции одной переменной

3.1. Производная функции, её геометрический и механический смыслы

Производной функции f(x) в точке х называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что последнее стремится к нулю, т.е. .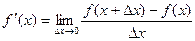

Функция y=f(x), имеющая производную в каждой точке интервала (а; b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием. Производная функции y=f(x)в произвольной точке х обозначается , , .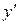

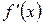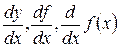При каждом конкретном числовом значении х производная (если она существует при данном х) функции y=f(x)представляет собой число.

Следствие:

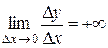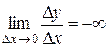1.Если для некоторого значения х или , то говорят, что для этого значения х существует бесконечная производная.

2. Если функция y=f(x) определена в левосторонней (правосторонней) окрестности точки х₀ и существует конечный или бесконечный предел этой функции 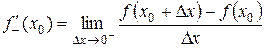( 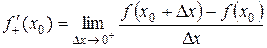), то она называется соответственно конечной или бесконечной производной слева (справа) функции f(x) в точке х₀.

Левую и правую производные называют односторонними производными.

3. Если функция f(x) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых, функция может иметь разрыв в точке х₀, а во- вторых, даже если функция непрерывна в точке х₀, она может быть в ней не дифференцируема.

4. Если функция y=f(x) имеет непрерывную производную 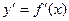в некотором интервале (a; b), то функция называется гладкой.

Например: f(x) = 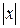- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема (Необходимое условие существования производной). Если функция f(x) имеет производную в точке х₀, то она непрерывна в этой точке.