Свойства функций, непрерывных на отрезке

1⁰ . (Первая теорема Вейерштрасса[2]). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие .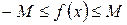

2⁰. Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

3⁰. (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

4⁰ .Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

5⁰ .(Первая теорема Больцано – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х₁Î[a,b] и x₂Î[a,b] таких, что ïх₂ – х₁ï< D верно неравенство ïf(x₂) – f(x₁)ï < e

Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.

6⁰ . (Теорема Кантора[3]) Функция, непрерывная на отрезке, равномерно непрерывна на нем (свойство справедливо только для отрезков, а не для интервалов и полуинтервалов).

Пример 24. .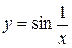

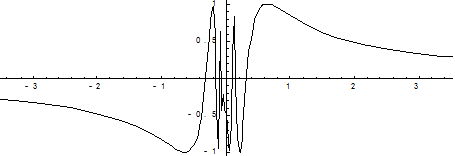
Рис. 9

Функция 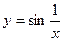непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х₁ и х₂ такие, чтоïf(x₁) – f(x₂)ï>e, e - любое число при условии, что х₁ и х₂ близки к нулю.

7⁰ . Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Пример 25. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

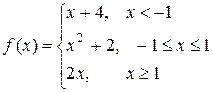
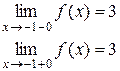
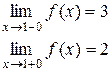
в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

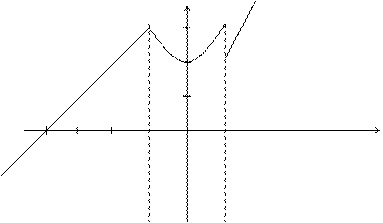у

-4 -1 0 1 х

Рис. 10