Первый замечательный предел
Первый замечательный предел: 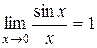 .
.
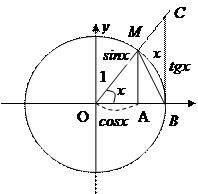 Доказательство.Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. Пусть
Доказательство.Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. Пусть 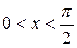 . На рисунке
. На рисунке 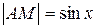 , дуга МВ численно равна центральному углу х,
, дуга МВ численно равна центральному углу х, 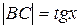 . Очевидно, имеем
. Очевидно, имеем 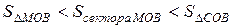 .
.
Рис. 4
На основании соответствующих формул геометрии получаем 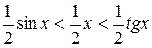 . Разделим неравенство на
. Разделим неравенство на 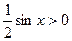 , получим
, получим 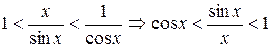 . Так как
. Так как 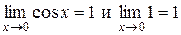 - то по признаку (о пределе промежуточной функции) существования пределов
- то по признаку (о пределе промежуточной функции) существования пределов 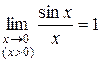 .
.
А так как 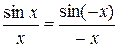 , то
, то 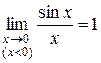
Пример 8. Найти 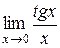 .
.
Решение. Числитель и знаменатель дроби при 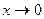 одновременно стремятся к нулю. Теорема о пределе дроби здесь неприменима. Для отыскания предела преобразуем данную дробь:
одновременно стремятся к нулю. Теорема о пределе дроби здесь неприменима. Для отыскания предела преобразуем данную дробь:
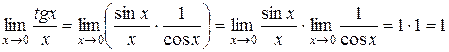 .
.
Пример 9. Найти 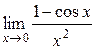 .
.
Решение. 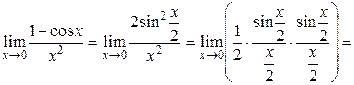
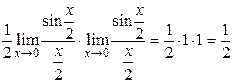 .
.
Второй замечательный предел
Второй замечательный предел: 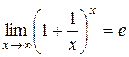
Докажем, что к числуестремится и функция xn = 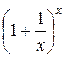 при
при 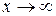 .
.
1. Пусть 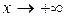 . Каждое значение х заключено между двумя положительными целыми числами:
. Каждое значение х заключено между двумя положительными целыми числами: 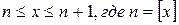 - это целая часть х. Отсюда следует
- это целая часть х. Отсюда следует 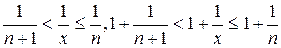 , поэтому
, поэтому 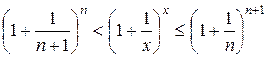 .
.
Если 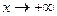 , то
, то 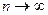 .
.
Поэтому имеем: 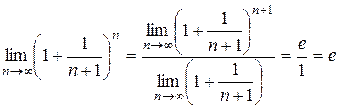 ;
;
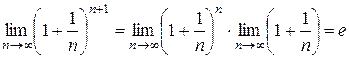 .
.
По признаку существования пределов 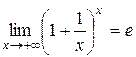 .
.
2. Пусть 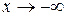 . Сделаем подстановку –х=t, тогда
. Сделаем подстановку –х=t, тогда
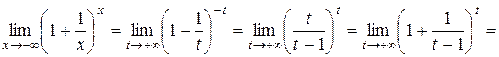
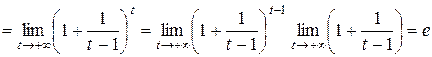
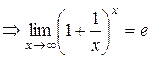 .
.
Пример 10. Найти 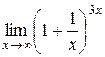 .
.
Решение.
1 способ. 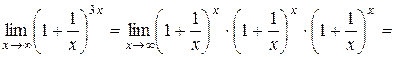
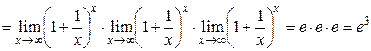 .
.
2 способ. 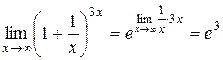 .
.
Замечание: для вычисления второго замечательного предела удобно пользоваться формулой 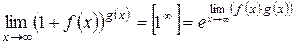 .
.
Пример 11. Найти 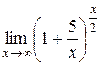 .
.
Решение. 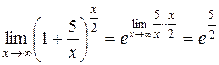 .
.
Пример 12. Найти 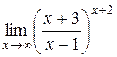 .
.
Решение.
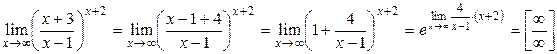 =
=
= 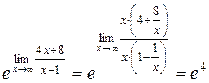 .
.
Дата добавления: 2017-12-05; просмотров: 934;
