Приложения дифференцирования функции одной переменной
4.1 Правило Лопиталя[4]
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и 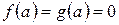 , то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует т.е.
, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует т.е. 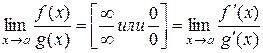 .
.
Пример 1.Вычислить пределы.
а) 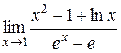 .
.
Решение. Как видно, при попытке непосредственного вычисления предела получается неопределенность вида 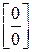 . Функции, входящие в числитель и знаменатель дроби, удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби, удовлетворяют требованиям теоремы Лопиталя.
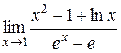 =
= 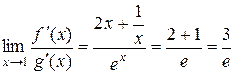 ;
;
б) 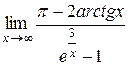 .
.
Решение. 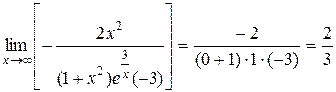 .
.
Замечание.
1. Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
2. Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере, с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
Пример 2.Найти предел 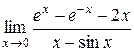 .
.
Решение. 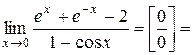
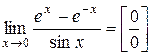 =
= 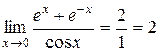 .
.
Неопределенности вида 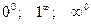 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 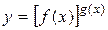 , f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции
, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции 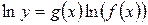
Пример 3. Найти предел 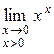 .
.
Решение.Здесь 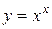 ,
, 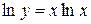 .
.
Тогда 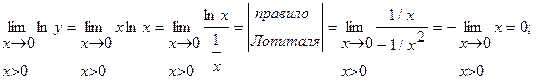 .
.
Следовательно 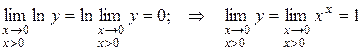
Дата добавления: 2017-12-05; просмотров: 459;
