Производная по направлению. Градиент.

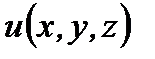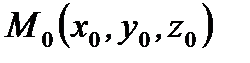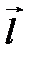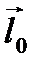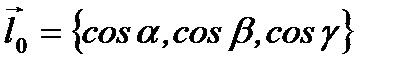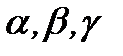Рассмотрим функцию трех переменных в некоторой окрестности точки . Через эту точку и через начало координат проведем ось , единичный вектор которой будет иметь координаты , где есть углы между осью 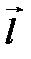и координатными осями 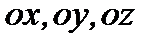. На оси 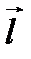возьмем точку 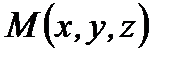и обозначим через 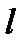величину направленного отрезка 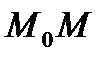(см. рис. 4.2).

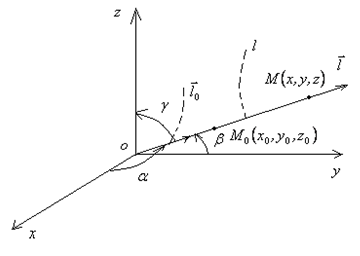
Рис. 4.2

Параметрические уравнения 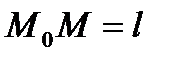будут иметь вид

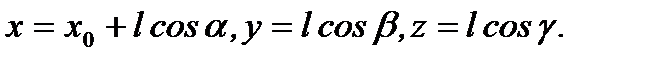(4.15) Тогда функция 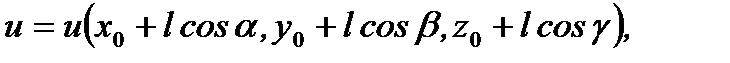то есть она является сложной

функцией от одной переменной 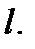Если фунция 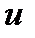имеет производную по 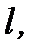то она называется производной по направлению и вычисляется по формуле

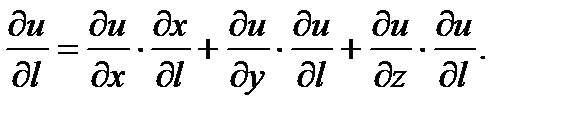(4.16)

Если учесть, что 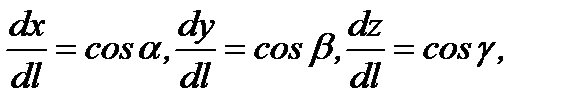то (4.16) можно переписать в виде

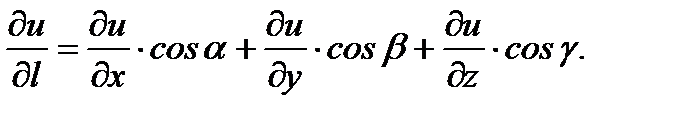(4.17)

Вектор с координатами 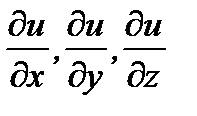в точке 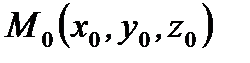называется градиентом функции 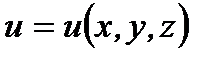в точке 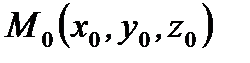и обозначается символом

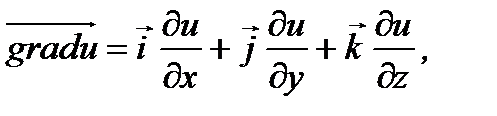(4.18)

где 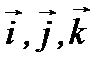есть единичные векторы осей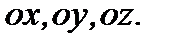

Заметим, что с учетом (4.18) выражение (4.17) можно переписать в виде скалярного произведения векторов 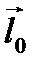и 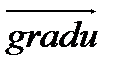, то есть

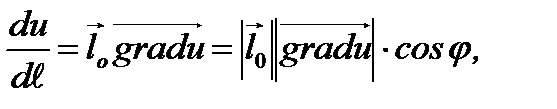(4.19)

где 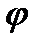есть угол между векторам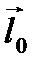и и 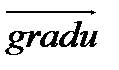. Так как 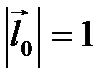, то

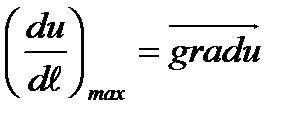
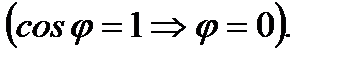(4.20)

Пример 4.12.Найти градиент функции 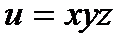в точке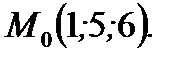

Решение.Найдем значения частных производных в заданной точке и подставим в (4.18). Имеем

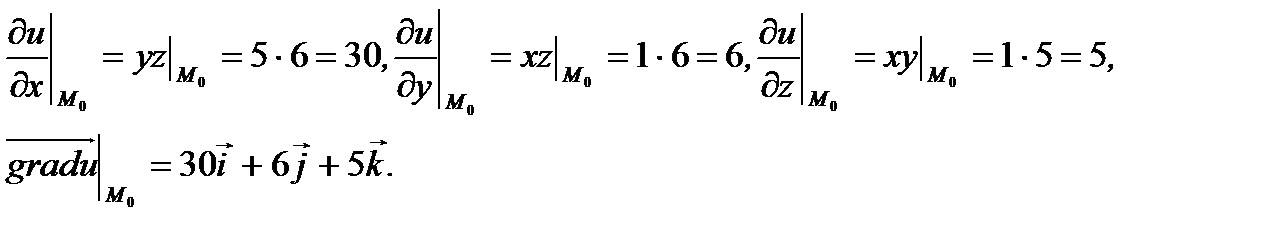
Ответ: