Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, приложенных к точкам системы.

Теорема в интегральной форме

Пусть механическая система переместилась из некоторого начального положения вконечное.

Тогда, интегрируя равенство (26) в пределах, соответствующих данному перемещению, получаем

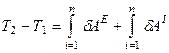
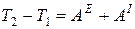. (28)

Соотношение (28) выражает теорему об изменении кинетической энергии системы в интегральной (конечной) форме:

Изменение кинетической энергии механической системы на некотором конечном перемещении равно сумме работ всех внешних и внутренних сил, действующих на точки системы, на этом перемещении.

Подчеркнем, что в отличие от теорем об изменении количества движения и кинетического момента механической системы, в теорему об изменении кинетической энергии входят внутренние силы.

В этом состоит принципиальное отличие этой теоремы от других.

В частном случае, когда механической системой будет абсолютно твердое тело, работа всех внутренних сил равна нулю, и уравнения (27), (28) принимают вид

, ,

.

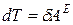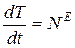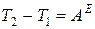Для материальной точки теорема об изменении кинетической энергии будет выражаться уравнениями

, ,

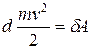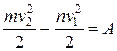где dА, А - соответственно элементарная работа и полная работа всех сил, приложенных к точке.