Производная сложной функции
Если 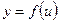 и
и 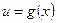 – дифференцируемые функции своих аргументов, то производная сложной функции
– дифференцируемые функции своих аргументов, то производная сложной функции 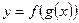 вычисляется по формуле
вычисляется по формуле
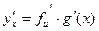 . (8)
. (8)
Обобщенная таблица производных:
1)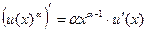 ,где
,где 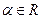 ,
,
в частности
а) 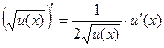 ,
,
б) 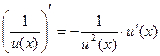 ;
;
2) 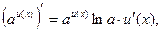 где
где 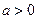 ,
,
в частности
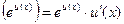 ;
;
3) 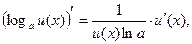 где
где 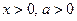 ,
,
в частности
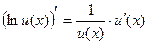 ;
;
4) 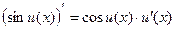 ;
;
5) 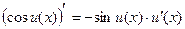 ;
;
6) 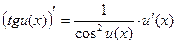 ;
;
7) 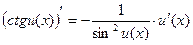 ;
;
8) 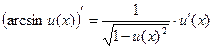 ;
;
9) 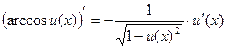 ;
;
10) 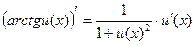 ;
;
11) 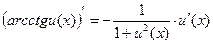 ;
;
12) 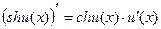 ;
;
13) 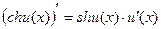 ;
;
14) 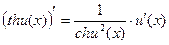 ;
;
15) 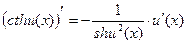 .
.
Если для функции 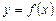 существует обратная функция
существует обратная функция 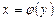 , которая имеет производную
, которая имеет производную 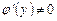 , то верна формула
, то верна формула
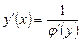 . (9)
. (9)
Пример 1:Найти производную функции:
1) 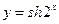 ; 2)
; 2) 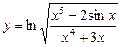 ;
;
3) 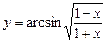 ; 4)
; 4) 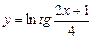 ;
;
5) 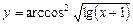 ; 6)
; 6) 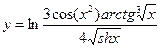
Решение. 1.Функцию 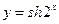 необходимо рассматривать как сложную функцию, где
необходимо рассматривать как сложную функцию, где 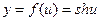 и
и 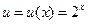 -- дифференцируемые функции своих аргументов. Тогда согласно формуле (8) и соответствующим формулам таблицы производных, получим:
-- дифференцируемые функции своих аргументов. Тогда согласно формуле (8) и соответствующим формулам таблицы производных, получим:
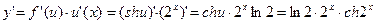
2. Сначала преобразуем функцию, используя свойства логарифмов:
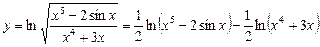
Вычисляем производную, используя правило дифференцирования суммы функций, формулу (8) и обобщенную таблицу производных:
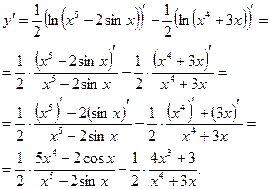
3.Рассмотрим функцию как 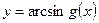 , где
, где 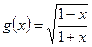 – также сложная функция. Применив формулу (8) дифференцирования сложной функции, обобщенную таблицу производных, а также правило дифференцирования частного двух функций, получим:
– также сложная функция. Применив формулу (8) дифференцирования сложной функции, обобщенную таблицу производных, а также правило дифференцирования частного двух функций, получим:
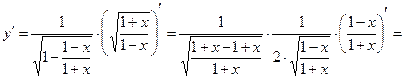
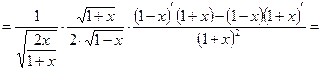
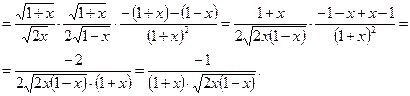 4.Пусть
4.Пусть 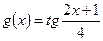 , тогда
, тогда 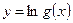 . Согласно формуле (8), получаем:
. Согласно формуле (8), получаем:
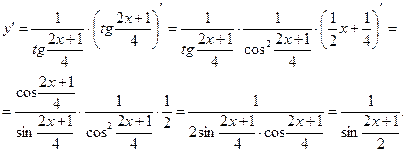 5.Рассмотрим функцию как
5.Рассмотрим функцию как 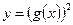 , где
, где 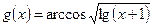 .
.
Функцию 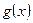 можно представить в виде
можно представить в виде 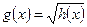 , где
, где 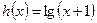 . Тогда:
. Тогда:
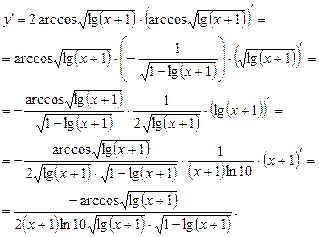
6.Перед тем как дифференцировать функцию, преобразуем выражение, пользуясь свойствами логарифма:
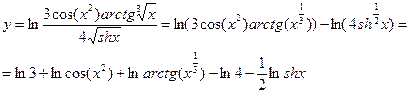 Продифференцируем полученное выражение по формулам (3), (4), (5), (8) и соответствующим формулам таблицы производных:
Продифференцируем полученное выражение по формулам (3), (4), (5), (8) и соответствующим формулам таблицы производных:
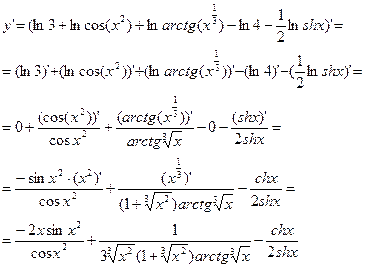
Применив далее формулы тригонометрии, окончательно получим:
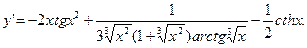
Пример 2. Вычислить 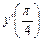 , если
, если 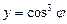 .
.
Решение
Это сложная функция с промежуточным аргументом 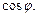 Дифференцируем её по формуле (8). При этом пользуемся первой формулой обобщенной таблицы производных при условии
Дифференцируем её по формуле (8). При этом пользуемся первой формулой обобщенной таблицы производных при условии 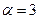 .
.
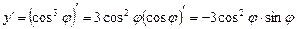
 .
.
Вычислим значение производной при 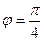 :
:
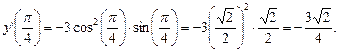
Пример 3.Вычислить 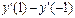 , если
, если 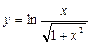
Решение
Преобразуем функцию, используя свойства логарифмов:
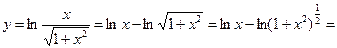
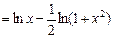 .
.
Теперь продифференцируем выражение по формулам (3), (5), (8) и соответствующим формулам таблицы производных. Функцию 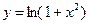 рассмотрим как
рассмотрим как 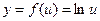 , где
, где 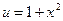 .
.
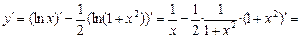
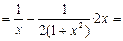
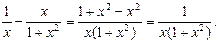
Теперь вычислим
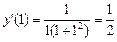 и
и 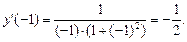
Тогда 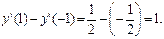
Дата добавления: 2017-09-19; просмотров: 490;
