Производная сложной функции

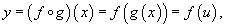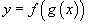Сложная функция записывается в виде: где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна 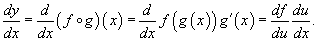Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции.

5. Вычисление производных функций Пример №1.Найти производную функции

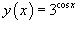Решение. Поскольку 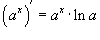то по правилу производной сложной функции получаем

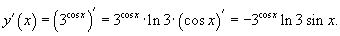
Пример №2.Найти производную функции 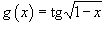. Решение. Здесь мы имеем дело с композицией трех функций. Производная тангенса равн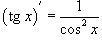а . Тогда

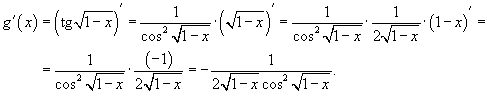
Пример №3.Определить производную функции 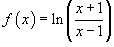. Решение. Применим формулы производной сложной функции и производной частного.

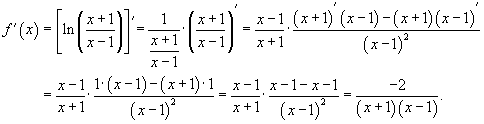
Пример №4.Продифференцировать функцию 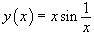. Решение. Сначала найдем производную произведения: 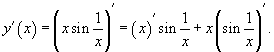Далее, по формуле производной сложной функции

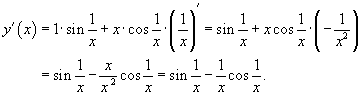
Пример №5.Продифференцировать 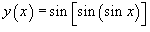. Решение. Здесь мы опять имеем дело с «трехслойной» функцией. Поэтому дважды применяем формулу производной сложной функции. Получаем

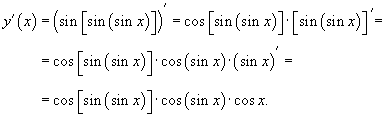
Пример №6. Найдите производные следующих функций:

а) y = sin² 3x

Т.к. данная функция сложная, то используем правило дифференцирования сложной функции y_x´= y_u´u_x´.

Порядок следования функций таков: y = u²; u = sinv; v = 3x

Значит y´ = (u²)´u_v´v´ = 2sin3x(sin3x)´(3x)´= 2sin3xcos3x3 = 3sin6x.

б)y = (x²+3x)⁵

y_x´ =y_u´u_x´= 5(х²+3х)⁴(х²+3х)´= 5(х²+3х)⁴(2х+3).

в)y = ln sin³5x

y´= (ln sin³5x)´(sin³5x)´(sin5x)´

Пример № 7. Найдите производную функции 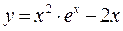и вычислите .

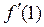Решение.

Пользуясь правилами дифференцирования, найдем производную: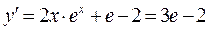

Вычислим .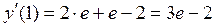

Пример № 8.

Найти производную функции и вычислить y’( .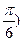

Решение.

y’

.

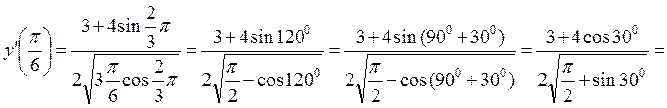
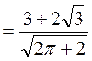Пример № 8.Вычислить приближенное значение функции y = x³ - 3x² + 30 при изменении аргумента от 3 до 3,002.

Решение.

При небольших изменениях аргумента (здесь приращение аргумента ∆x = 3,002-3 = 0,002 небольшое) можно воспользоваться формулой приближенного значения функции f(x₀+∆x)≈f(x₀)+f’(x₀) ∆x Примем f(x) = y = x³-3x² +30, тогда f’(x) = 3x²-6x, положим x₀ = 3, ∆x = 0,002. Вычислим f(x) = 3³-3∙3²+30 = 30; f’(3) = 3∙3²-6∙3 = 9. Тогда, по формуле будем иметь f(3,002) ≈30+9∙0,002 = 30+0,018 = 30,018.