Метод половинного деления (дихотомия)

Дихотомия применяется, когда требуется надежность счета, а скорость сходимости не имеет значения.

f(х_n+1)

Y

f(х_ср)

х_n х_cр2 х^* х_cр1 х_n+1 Х

f(х_n)

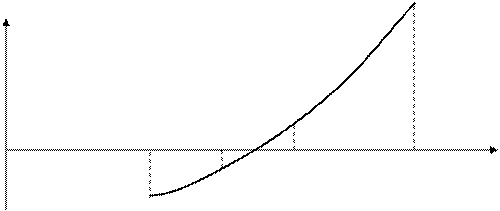
Рисунок 5.2 – Геометрическая интерпретация метода дихотомии

Пусть дано уравнение f(x)=0 и отделен простой корень х^*, то есть найден такой отрезок [х_n, х_n+1], х^* принадлежит [х_n, х_n+1] и на концах интервала функция имеет значения, противоположные по знаку. Отрезок

[х_n, х_n+1] называется начальным интервалом неопределенности,потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.

Алгоритм метода дихотомии.

1. Вычисляют значения функции через равные интервалы значений х до смены знака, при переходе от f(x_n) к f(x_n+1)

2. Вычисляют среднее значение аргумента x_ср и находят f(x_ср).

3. Если знак f(x_ср) совпадает со знаком f(x_n), то в дальнейших расчетах вместо x_n используют x_cp. Если f(x_cp) совпадает с f(x_n+1), то вместо x_n+1 берут x_cp.

4. Интервал, в котором заключено значение корня, сужается. Если f(x_cpk) ≤ 0 + ε, где ε положительное наперед заданное достаточное малое число – точность расчета, то процесс заканчивается за k итераций, при этом ширина интервала уменьшается в 2^k раз. Если f(x_cpk) > 0 + ε, повторяют пп.2-3 алгоритма.

Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза.

Метод не применим к корням четной кратности, т.е. тогда когда, f(x)=g(x)(x-x₁)^m, где x₁ корень кратности m.

Метод хорд

В основе этого метода, как и в методе дихотомии, лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки, но он обеспечивает более быстрое нахождение корня.

Y f(х_n+1)

x₁^* x₂^* x₃^* x₄^* x^*

х_n х_n+1 X

f(х_n)

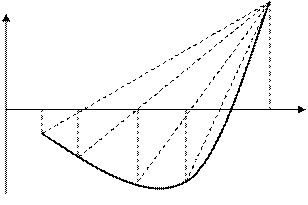
Рисунок 5.3 – Геометрическая интерпретация метода хорд

Алгоритм метода хорд.

1. Вычисляют значения функции через равные интервалы значений х до смены знака при переходе от f (x_n) к f (x_n+1).

2. Прямая, проходящая через эти две точки, пересекает ось х в точке

х^* = x_n – f (x_n)( x_n+1 - x_n)/ (f (x_n+1) – f (x_n)) (5.1)

3. Находят значение f (x_k^*), которое сравнивают с известными f (x_n),

f (x_n+1). Если знак f(x_к^*) совпадает со знаком f(x_n), то в дальнейших расчетах вместо x_n используют x_k^*. Если f(x_k^*) совпадает с f(x_n+1), то вместо x_n+1 берут x_k^*.

4. Проверяют близость f(x_k^*) к нулю c заданной точностью ε. Если f(x_k^*) ≤ 0 + ε, то процесс заканчивается за k итераций. Если f(x_k^*) > 0 + ε, повторяют пп.2-3 алгоритма.

В знаменателе формулы (5.1) стоит разность значений функций. Вдали от корня она несущественна, но вблизи корня эти значения близки и малы. Возникает потеря значащих цифр, приводящая к «разболтке» счета. Это ограничивает точность, с которой можно найти корень. Для простых корней это ограничение невелико, а для кратных – существенно. Можно использовать метод Гарвика. Выбирают не очень малое ε, ведут итерации до выполнения условия |x_n+1 - x_n| < ε и затем продолжают расчет до тех пор, пока |x_n+1 - x_n| убавает.

Метод Ньютона

Метод последовательных приближений, разработанный Ньютоном, используется наиболее часто среди всех итерационных алгоритмов.

Функция f(x), дважды дифференцируемая на отрезке [a, b], который содержит корень х^*. При этом f(x^*)=0. Для определения интервала, в котором заключен корень, в методе Ньютона не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции будем проводить экстраполяцию с помощью касательной в данной точке.

Y

М₀

х^*

X

х₁ х₂ х₀

М₁

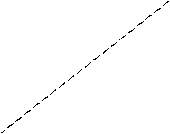
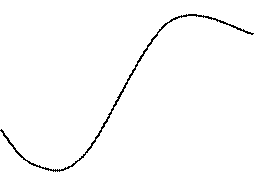
Рисунок 5.4 – Геометрическая интерпретация метода Ньютона

Алгоритм метода:

1. Находят значение x_n+1, которое соответствует точке, в которой касательная к кривой в точке x_n пересекает ось х

x_n+1 = x_n - f(x_n)/f ′(x_n) (5.2)

2. Процедуру повторяют до выполнения условия близости функции к нулю с заданной точностью f(x_n) ≈ ε

Быстрота сходимости метода Ньютона в большой мере зависит от выбора исходной точки. Если в процессе итераций тангенс угла наклона касательной f ′(x_n) обращается в ноль, то применение метода усложняется. В случае бесконечно больших f ′′(x) метод также недостаточно эффективен. При кратности корней (условие f (x)=f ′(x)=0) метод Ньютона не обеспечивает сходимости.

Метод секущих

Одним из недостатков метода Ньютона является необходимость дифференцирования заданной функции f(x). Если нахождение производной затруднено, можно воспользоваться некоторым приближением, которое положено в основу метода секущих. Заменим производную f ′(x_n) для расчета

x_n+1 = x_n - f(x_n)/f ′(x_n) разностью последовательных значений функции, отнесенных к разности последовательных значений аргумента, т.е. разделенной разностью первого порядка

F*(x_n)= (f(x_n)- f(x_n-1))/( x_n- x_n-1),

тогда

x_n+1 = x_n - f(x_n)/ F*(x_n). (5.3)

Схема алгоритма остается, как и в методе Ньютона, изменяется только вид итерационной формулы (5.3).

5.6 Метод простой итерации (последовательных приближений)

Для применения этого метода уравнение f(x)=0 приводится к виду

х = g(х). Задаются начальным значением х₀, а последующие приближения вычисляются с помощью итерационной процедуры

x_n+1= g(х_n). (5.4)

Для сходимости метода необходимо выполнение условия

0< g′ (х_n)<1

Y

x

g(x)

X

х₀ х₁ х₂

Рисунок 5.5 – Геометрическая интерпретация метода простых итераций

Компьютерная реализация методов в Excel описана в [9], [23-24, 26].

Литература: [1-4],[6], [9], [14-17], [23-24].

Лекция 6

Тема: Численные методы решения систем алгебраических уравнений

План: Постановка задачи нахождения решения систем линейных и нелинейных алгебраических уравнений. Примеры решения систем уравнений в теплоэнергетических расчетах. Методы решения систем алгебраических уравнений (Гаусса, Зейделя, Ньютона).