Задача Коши для обыкновенного дифференциального уравнения первого порядка

Уравнение, содержащее одну или несколько производных, называют дифференциальным. Поскольку большинство физических законов науки и техники записаны в форме дифференциальных уравнений, их решение является повседневной необходимостью. Задачи моделирования, связанные с движением массы или энергии, теплотехнологическими процессами и теплоэнергетическими системами, изменяющимися во времени, также неизбежно ведут к дифференциальным уравнениям. К сожалению, число уравнений, которые можно успешно решить аналитическими методами, очень ограничено. Поэтому при рассмотрении научных и инженерных задач особенно важен вопрос о решении дифференциальных уравнений с помощью персонального компьютера.

В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных, дифференциальные уравнения делятся на две категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называют частными.

Дифференциальным уравнением называется уравнение, содержащее неизвестные функции у, независимые переменные x, производные неизвестных функций:

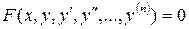(7.1)

Решить дифференциальное уравнение - найти его общий интеграл - функцию Ф, связывающую независимую переменную х, искомую функцию у и n постоянных интегрирования с помощью уравнения Ф(х,у,с₁,. с₂,….,с_n) = 0.

Чтобы решить обыкновенное дифференциальное уравнение (ОДУ), необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия заданы при одном значении независимой переменной, то такую задачу называют задачей с начальными условиями или задачей Коши. Если же условия заданы при двух значениях независимой переменной, задачу называют краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче ¾ граничными.

Численное решение – это построение таблицы приближенных значении у₁,y₂, y₃,…, y_n. решения уравнения y = f (x) в точках x₁,x₂,x₃,…x_n.

Чаще всего полагают x_i = x₀+ih, где i = 0,1,2…n. Точки x_i носят название узлов сетки, а величина h – шага сетки.

Численные методы разделяются на одношаговые, дающие формулу для вычисления значения y_k+1 по одному предыдущему значению y_k, и многошаговые, при которых для вычисления значения y_k+1 требуется k предыдущих значений функции у_l,y_l-1, y_l-2,…, y_l-(k+1).

К одношаговым относятся методы Эйлера и Рунге-Кутты, к многошаговым – методы прогноза и коррекции.

Для оценки погрешности метода на одном шаге сетки разложим точное решение уравнения в ряд Тейлора в окрестности узла x_k:

y(х_k+1)= y(х_k)+ (h/1!) y'(х_k)+ (h²/2!) y''(х_k) +….+(h^р/р!) y^(р)(х_k)+.. . (7.2)

Численный метод решения дифференциального уравнения имеет порядок р, если его расчетные формулы согласуются с разложением в ряд Тейлора до членов порядка h^р. Погрешность, связанная с тем, что вместо бесконечного ряда, рассматривается аппроксимация функции несколькими первыми членами ряда, называется погрешностью усечения (ограничения). Источником погрешностей будет представление чисел с ограниченным числом значащих цифр – погрешности округления и погрешность распространения – результат накопления погрешностей, появившихся на предыдущих этапах счета.