Задачи оптимизации в теплоэнергетике и теплотехнике
Решение многих теоретических и практических задач теплоэнергетики сводится к отысканию экстремума (максимума или минимума) скалярной функции f(x) n-мерного векторного аргумента х.
| х = | х1 х2 х3 … хn |
х – вектор-столбец (точка в n-мерном пространстве).
Например: достижение максимального КПД котельного агрегата; обеспечение минимальной себестоимости тепловой энергии, отпускаемой ТЭЦ; обеспечение минимального значения теплопотерь через теплоизоляцию теплопровода, обмуровку котла, оболочку здания; достижение минимального значений выбросов загрязняющих веществ ТЭС и т.п.
Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности.
В дальнейшем мы будем говорить о поиске минимального значения f(x)
| f(x) | 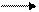
| min |
Вектор х*, доставляющий min целевой функции f(x), называют оптимальным.
Задачу нахождения минимума функции f(x) можно заменить эквивалентной задачей поиска максимума функции - f(x).
Если х* - точка минимума для функции у=f(x), то для функции у = -f(x) она является точкой максимума
min f(x) = -max (- f(x)),
аналогично и для случая многих переменных.
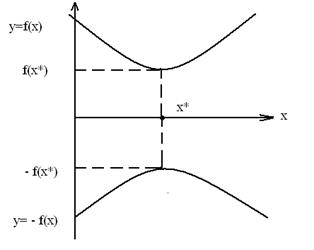
Рисунок 9.1 –Графическая интерпретация поиска экстремума функции
В реальных условиях на переменные хi , i=1,2, .. n и некоторые функции gi(x) и hj(x), характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:
gi(x) = 0, i = 1,2, .. n
hj(x) £ 0, j = 1,2, .. m
a £x £b,
где
| а = | а1 а2 а3 … аn |
| b = | b1 b2 b3 … bn |
, .
Такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.
Точка х* доставляет глобальный минимум функции одной переменной f(x), заданной на числовой прямой Х, если х ÎХ и f(x*) £ f(x) для всех х ÎХ.
Точка х* называется точкой строгого глобального минимума, если это неравенство выполняется строго.
Если же в выражении f(x*) £ f(x) равенство возможно при х ¹ х*, то реализуется нестрогий минимум,а под решением в этом случае понимают х* ={ х ÎХ : f(x) = f(x*)}.
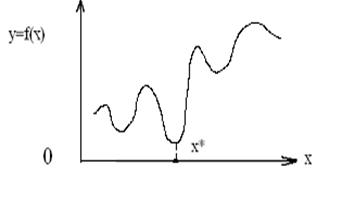
Рисунок 9.2 –Глобальный минимум функции одной переменной
Рисунок 9.3 –Нестрогий минимум функции одной переменной
Точка х*ÎХ доставляет локальный минимум функции f(x) на множестве Х, если при некотором достаточно малом ε > 0 для всех х ¹х*, хÎХ, удовлетворяющих условию | х-х*| < ε , выполняется неравенство f(x*) ≤ f(x), если неравенство строгое, то х* является точкой строгого локального минимума.
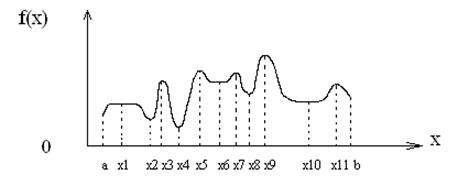
Рисунок 9.4 –Экстремумы функции одной переменной на участке [a,b]
На рисунке 9.4: х1, х3, х5, х6, х7, х11 – точки локального максимума (х1 – нестрогого); х2, х6, х8, х10 (х6-нестрогого) – локального минимума; х4 - глобального минимума; х9 – глобального максимума.
Дата добавления: 2017-09-19; просмотров: 1580;
