Одношаговые методы решения задачи Коши

Различные методы данной группы отличаются объемом проводимых вычислений и получаемой при этом точностью

Метод Эйлера

Дано уравнение у' = f(x,y) с начальным условием у(х₀)= у₀.

В методе Эйлера производная у' заменяется приближенной формулой

у'= Δу/Δх = f(x,y)

В результате на первом отрезке [х₀,х₁] искомое решение приближенно представляется линейной функцией

Δу/Δх = f(x₀,y₀),

или у-у₀ = f(x₀,y₀)(х-х₀), у = у₀ + f(x₀,y₀)(х-х₀).

При х=х₁ получим

у₁ = у₀ + f(x₀,y₀)(х₁-х₀).

Таким образом, на отрезке [х₀,х₁] искомая интегральная кривая (точное решение) заменяется отрезком прямой ММ₀, касательной к кривой в точке М₀.

Тангенс угла наклона этой прямой равен f(x₀,y₀). Аналогично находят остальные приближенные значения

y_i+1 = у_i + K₁h, (7.3)

где K₁=f(x_i,y_i), h=(х_i-х_i-1).

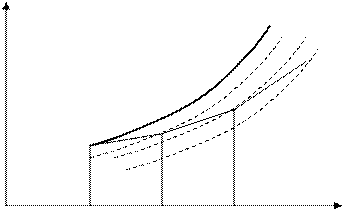
Из (7.3) следует, что интегральная кривая в методе Эйлера заменяется ломаной линией с вершинами в точках М₀(x₀,y₀), М₁(x₁,y₁),…, М_n(x_n,y_n) (рис.7.1).

Метод Эйлера является наиболее простым и наименее точным методом решения ОДУ. Он применяется для поиска оценочных решений на [х₀,х_n].

У

у(х)

М₂

М₁

М₀

Х

х₀ х₁ х₂

Рисунок 7.1-Геометрическая интерпретация метода Эйлера

В рассмотренном методе переход от точки (x_i,y_i), в точку (x_i+1,y_i+1), осуществляется путем смещения на вектор (h, К₁). Ошибка метода имеет порядок h², так как члены, содержащие h во второй и более высоких степенях, отбрасываются, кроме того метод часто оказывается неустойчивым – малая ошибка увеличивается с ростом х. Этот метод можно усовершенствовать различными способами [1].

Рассмотрим модифицированный метод Эйлера. Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен y¢(x₀), он изменяется в соответствии с изменением независимой переменной. Поэтому в точке (x₀+h) наклон касательной уже не таков, каким он был в точке x₀. Следовательно, при сохранении начального наклона касательной на всем интервале h в результаты вычислений вносится погрешность. Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала вычисляют значение функции в следующей точке по методу Эйлера

y*_n+1=y_n + hf (x _n, y _n ). (7.4)

Его используют для вычисления приближенного значения производной в конце интервала f(x_n+1,y*_n+1). Вычислив среднее между этим значением производной и ее значением в начале интервала, найдем более точное значение y_n+1:

y_n+1=y_n+ (f (x_n, y_n)+f (x_n+1,y*_n+1))/2h. (7.5)

Модифицированный метод Эйлера имеет второй порядок точности, т.е погрешность метода имеет порядок h³.

Методы Рунге-Кутты

Наибольше распространение при решении обыкновенных дифференциальных уравнений получилметоды Рунге-Кутты.

В методах Рунге-Кутты более высокого порядка точности смещение из

точки (x_i,y_i), в точку (x_i+1,y_i+1) происходит не сразу, а через промежуточные точки (внутренние для интервала [х_i,х_i+1]), в каждой из которых определяется направление касательной. В результате смещение выполняется вдоль некоторого усредненного направления. Методы Рунге-Кутты дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге-Кутты, в сущности, объединяет целое семейство методов решения дифференциальных уравнений первого порядка, которым можно отнести метод Эйлера и его модификации.

Наиболее распространенным является метод Рунге-Кутты четвертого порядка точности, для которого ошибка на шаге имеет порядок h⁵.

В этом методе значения величины y_i+1 рассчитывается по формуле

y_i+1=y_i+h (K₁+2K₂+2K₃+K₄)/6, (7.6)

где K₁=f (x _i, y_i),

K₂=f (x_i+ h /2,y_i+ h k₁/2),

K₃=f (x_i+ h /2, y_i+ h k₂/2),

K₄=f (x_i+h, y_i+ h k₃).

Метод Рунге-Кутты применим к системам уравнений первого порядка, а также к уравнениям любого порядка, которые можно свести к системам уравнений первого порядка путем замены переменных.