Тогда формула для погрешности
f(x) - Pn(x) = 
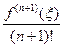
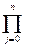(x-xj), 
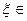[a,b].
Формула (3) содержит значения функций в узлах интерполяции, она применима как для равноотстоящих, так и для неравноотстоящих узлов. К недостаткам формулы можно отнести то, что при изменении числа узлов все расчеты необходимо проводить заново.
При вычислениях на РС в том случае, когда шаг сетки постоянен, удобна интерполяционная формула Ньютона.Для ее записи надо ввести так называемые разделенные разности.
Разделенная разность нулевого порядка совпадает со значением функции в узлах.
Разделенная разность первого порядка определяется так
у(xi, xj) = [y (xi) - y(xj)]/(xi - xj).
Разделенная разность второго порядка –
y(xi,xj,x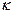 
) = [y(xi,xj) - y(xj,x 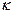)]/(xi - x 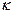) и т.д.
Тогда функция-интерполянта приобретает вид
f(x) = yo +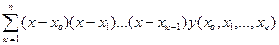 
(3.4)
Уравнение (3.4) определяет полином Ньютона.
После того как вычислены разделенные разности, вычислять полином Ньютона удобно по схеме Горнера:
f(x) = y(xo) + (x-xo) [y (xo,x1) + (х-х1) [y (xo,x1,x2) + …]] (3.5)
Вычисление f(x) по (3.5) для каждого х требует n умножений и 2n сложений и вычитаний.
Следует иметь в виду, что применение полинома высокой степени может приводить к трудным проблемам, связанным с погрешностями округления.
Важным вопросом является сходимость интерполяции, т.е. выяснение условий, при которых погрешность метода стремится к нулю. Для уменьшения погрешности можно сохраняя степень интерполяционного полинома уменьшать шаг сетки, либо, сохраняя шаг сетки, увеличивать число используемых узлов, т.е. степень многочлена.
На практике, если 3-5 узлов не обеспечивают требуемой точности, то нужно не увеличивать число узлов, а уменьшить шаг таблицы.
Для данного порядка интерполяции n ошибка имеет порядок n.
Ошибка ограничения или «усечения» (разложение в ряд «усечено» до некоторого порядка) определяется так
εr = sup|f(x)-P(x)| = hnM/n!, h = |xn-x1|, M = sup|fn(x)|
К ошибке ограничения добавляют ошибку округления.
Дата добавления: 2017-09-19; просмотров: 453;