Влияние погрешности регистрации статистических данных на

точность регрессионной модели[4]

Независимые переменные измеряются с ошибками:

X_i = X⁰_i + e_i ,

где e_i –ошибка измерения; X⁰_i – истинное значение контролируемой переменной.

Ошибка имеет нормальный закон распределения:

e_i ≈(0, ξ_i²).

Рассчитанная по данным наблюдениям модель оценивается остаточной дисперсией:

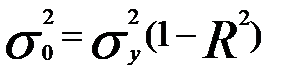
где 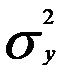- дисперсия выходной переменной, не зависит от ошибки измерения x_i.

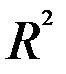- коэффициент детерминации подвержен влиянию ошибок измерений x_i:

R² = R²_y,x1,x2,..xk .

Составим матрицу (Х^тХ)^-1 коэффициентов ковариации:

y x₁ x₂ …. x_k

y d_yy d_y1 d_y2……d_yk

x₁ d₁₁ d₁₂……d_1k

D= x₂ d₂₂ …. d_2k

.

.

x_k d_kk

где d_yy =σ_y²; d_yj = Cov(y, x_j) ; d_ij = Cov(x_i ,x_j).

Тогда множественный коэффициент корреляции равен:

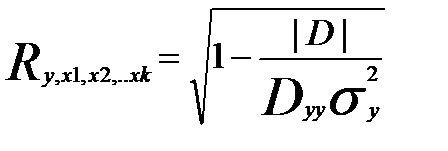
где |D| - определитель матрицы D;

D_yy - алгебраическое дополнение элемента d_yy матрицы D.

Для упрощения расчетов коэффициентов линеаризованного регрессионного уравнения выполним центрирование всех переменных. Тогда уравнение примет вид:

(y – y_cp) = b₁(x₁ – x_1cp) + …..+ b_k(x_k – x_kcp) + e.

Матрица для записи коэффициентов нормальных уравнений принимает вид:

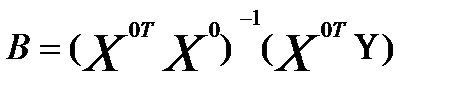
Корреляционная матрица для центрированных значений переменных равна:

x₁⁰ x₂⁰ …… x_k⁰

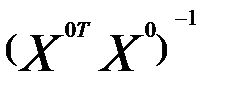
= x₂⁰ d₂₂ …… d_2k (1)

.

.

x_k⁰ d_kk

Дополнив первую строку и столбец (1) коэффициентами ковариации центрированных значений зависимой переменной с факторными переменными, получим матрицу D⁰:

y⁰ x⁰₁ x⁰₂ x⁰_k

y⁰ d⁰_yy d⁰_y1 … .d⁰_yk

x₁⁰ d⁰_1y d⁰₁₁ ……d⁰_1k

D⁰ = x₂⁰ d⁰_2y d⁰₂₂ d⁰_2k (2)

.

.

x_k⁰ d⁰_ky d⁰_kk

где d⁰_yy= σ_y0²; d⁰_yj = Cov (y⁰, x⁰_j); d⁰_ij = Cov(x⁰_i ,x⁰_j).

Коэффициенты уравнения регрессии рассчитываются через определитель матрицы D⁰ (2) по формуле:

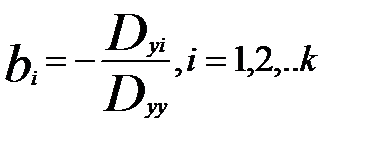
где 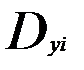- алгебраическое дополнение элемента d⁰_yj матрицы D⁰;

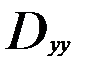- алгебраическое дополнение элемента d⁰_yy матрицы D⁰.

Рассмотрим влияние ошибок измерения факторных переменных на оценки b_i :

d_ij = Cov{(x⁰_i + e_i ), (x⁰_j + e_j )}= Cov{(x⁰_i ), (x⁰_j )} = d⁰_ij ;

d_ii = Cov{(x⁰_i + e_i ), (x⁰_i + e_j )}= Cov{(x⁰_i ), (x⁰_i )} + 2Cov{x⁰_i, e_i} +

+ Cov{e_i e_i} = d⁰_ii + ξ²_i ;

d_yi =Cov{(y⁰ + e_y) , (x⁰_i + e_i )} = d⁰_yi .

Под влиянием ошибок измерений в матрице D⁰(2) изменяются значения диагональных элементов (возрастают). Недиагональные элементы не изменяются. Рассмотрим, как это скажется на коэффициенте детерминации R²:

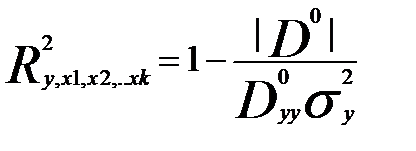
Для выявления зависимости коэффициента детерминации от погрешностей измерения x⁰_i рассмотрим частные производные, используя теорему о дифференцировании определителей:

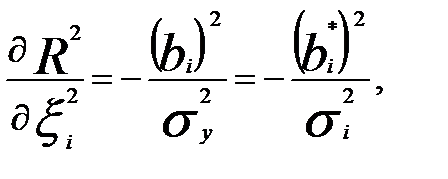
где 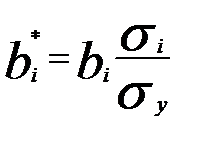- регрессионные коэффициенты при стандартизации факторных переменных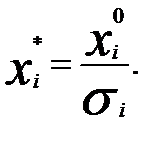

Знак минус производной указывает, что погрешность измерений факторных переменных приводит к уменьшению коэффициента детерминации.

Заменяя дифференциал на приращения, получаем:

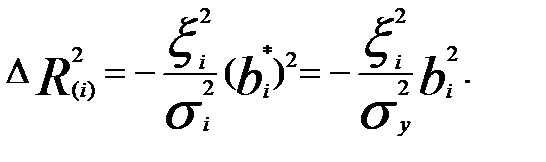
Вывод:

1. Чем больше размах колебаний факторных переменных, тем меньше сказывается влияние погрешности регистрации e²_i на точность регрессионной модели.

2. Погрешность измерения зависимой переменной оказывает влияние на точность модели

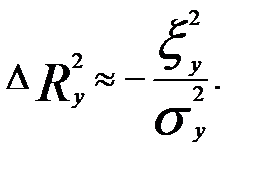
Практические рекомендации: чем больше размах колебаний факторных переменных, тем меньше сказываются погрешности измерений на точность регрессионной модели.

На основе теоремы о полном приращении функции многих переменных можно записать:

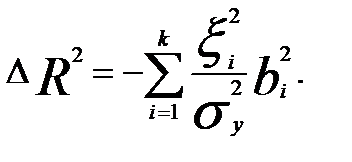
Запишем формулу остаточной дисперсии уравнения регрессии:

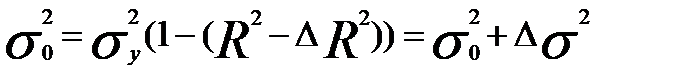
Погрешности измерений факторных переменных приводят к увеличению остаточной дисперсии уравнения регрессии. Ошибки измерений снижают эффективность м.н.к. оценок:

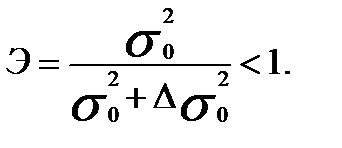
Оценим влияние погрешностей регистрации факторных переменных на коэффициенты регрессии [4]:

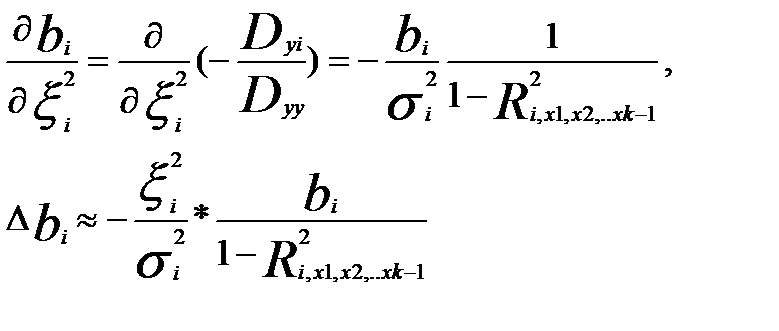
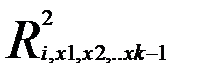- множественный коэффициент корреляции факторной переменной x_i с остальными факторными переменными.

Ошибки измерения факторных переменных приводят к уменьшению значений коэффициентов регрессии. Чем теснее связь между переменными

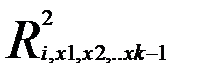, тем влияние сильнее.

Ошибки измерения зависимой переменной у не влияют на значения коэффициентов регрессии:

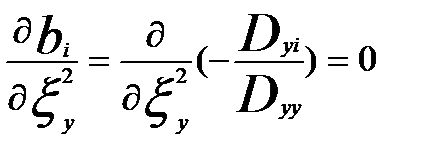
Оценим чувствительность регрессионного коэффициента b_i к ошибкам измерений других факторных переменных:

Полное приращение (+/-) ∆b_i за счет ошибок в остальных факторных переменных равно:

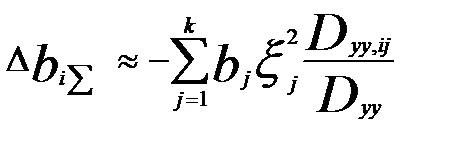
При некоррелированности факторных переменных 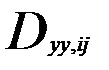=0, получаем

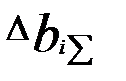=0. В этом случае ошибки регрессионных коэффициентов ∆b_i будут вызываться только ошибками измерений самих переменных x_i.:

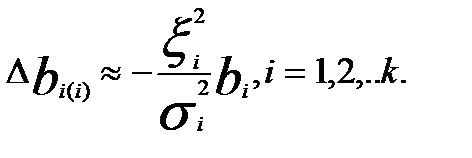
Вычисленные коэффициенты регрессии получаются асимптотически смещенными. С увеличением числа опытов дисперсия оценок коэффициентов регрессии уменьшается:

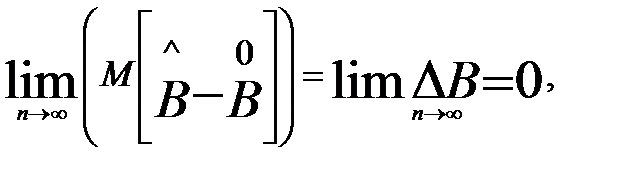
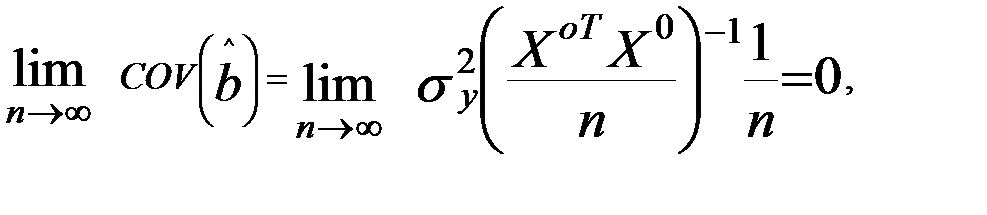
При этом оценки не сходятся к истинным значениям, т.е. оценки не состоятельные.

Степень искажения оценок коэффициентов регрессии можно судить по следу матрицы А, составленной по центрированным значениям факторных переменных (без ошибок):

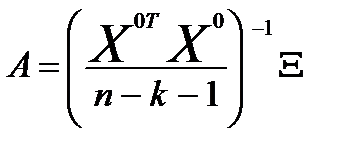
где - матрица ошибок факторных переменных.

След матрицы А равен:

,

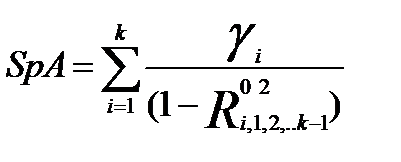где 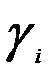- относительная точность измерения факторных переменных x_i .

Смещение оценок и увеличение их дисперсии за счет ошибок измерения факторных переменных малы при выполнении условий:

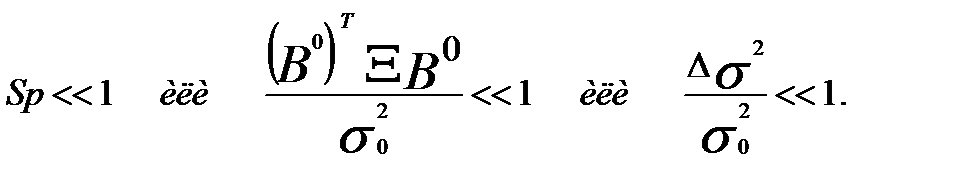
Контрольные вопросы

1. В чем особенность планирования промышленного эксперимента?

2. Как определяется продолжительность эксперимента и дискретность съема данных с объекта?

3. Как сказывается погрешность регистрации данных на коэффициенте детерминации модели регрессии?

4. Как влияют ошибки измерения независимых переменных на коэффициенты уравнения регрессии?

5. Как число опытов влияет на дисперсию коэффициентов регрессии?

6. Что необходимо предпринимать для уменьшения влияния погрешностей измерения независимых переменных на точность модели регрессии?

Лекция 8Рекуррентные алгоритмы построения математического описания дрейфующих объектов. Метод текущего регрессионного

Анализа

При построении математического описания промышленных объектов приходится встречаться с фактом неконтролируемого изменения характеристик объекта во времени. Объекты, обладающие такими свойствами, называются нестационарными (дрейфующими). Причиной являются наличие неконтролируемых воздействий, значения которых не могут учитываться при построении модели объекта. Дрейф характеристик может возникать из-за изменения активности катализатора, износа огнеупоров тепловых агрегатов, изменения условий работы, влияние времен года и др. Как правило, изменение дрейфующих параметров происходит значительно медленнее процесса изменения контролируемых переменных.

В предыдущих лекциях при построении математического описания по выборке оценивались математические ожидания коэффициентов модели в предположении отсутствия дрейфа. Будем рассматривать случай, когда действительные значения коэффициентов изменяются во времени. Для этого выбирается адаптивный путь решения задачи, в котором по выборке необходимо получить помимо математического ожидания коэффициентов оценки рядя параметров, значения которых определяются неизвестными априори свойствами дрейфа [4].

При решении задачи построения математического описания дрейфующего объекта возможны ситуации двух типов:

1) по выборке наблюдений за входом и выходом объекта на некотором интервале времени от t₀ до t>t₀ необходимо найти оценки вектора коэффициентов модели, близкие к действительным значениям коэффициентов в момент t+α, где α≥0;

2) осуществляется непрерывное слежение за изменением коэффициентов модели. В любой момент времени t требуется найти наилучшее приближение к действительным значениям коэффициентов в момент t+α.

Вторая ситуация аналогична первой при стремлении длины интервала наблюдений к бесконечности.