Поверхностей отклика

На практике часто приходится отыскивать условный экстремум функции отклика 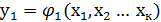при ограничениях, накладываемых другой функцией y₂=φ₂=(x₁, x₂,..x_k)[2].

При большом числе независимых переменных задача решается методом неопределенных множителей Лагранжа.

Метод неопределенных множеств Лагранжа сводится к решению системы уравнений:

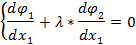
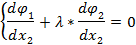
… (9)

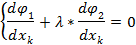
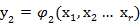
относительно переменных х₁, х₂, ..x_k, λ при некотором фиксированном значении y₂.

Пример 3.

Для выхода реакции y₁ и чистоты продукта y₂ получены уравнения регрессии [2]:

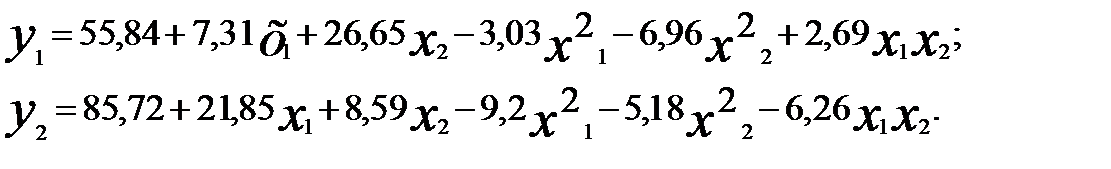
где 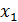– давление, 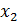– температура химического процесса.

Задавшись частотой продукта у₂=90%, находим условный экстремум для функции, определяющий выход реакции у₁.

Метод неопределенных множеств Лагранжа приводит к системе уравнений:

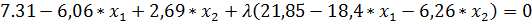
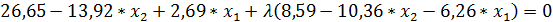
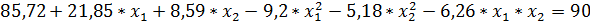
Методом скорейшего спуска были найдены три решения (табл. 2).

Анализ табличных данных показывает, что чистота продукта у₂ может быть достигнута за счет уменьшения выхода реакции у₁.

Таблица 2 – Результаты решения задачи на условный экстремум [2]

Варианты решений
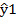
	83,66	86,73	88,68
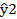
	94,87	92,47	89,99
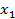
	0,965	1,005	1,075
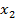
	1,088	1,316	1,479
λ	1,612	0,973	0,665

В ряде случаев при решении подобных задач сталкиваются со специфическими вычислительными трудностями, связанными с тем, что матрицы оказываются плохо обусловленными (определитель матрицы (X^тX) близок к нулю). Результаты вычислений при этом становятся неустойчивыми. Имеются ряд приемов, позволяющие преодолеть эти трудности [2].

Контрольные вопросы

1. Когда возникает задача поиска оптимальных условий протекания процесса?

2. При решении задачи используется математиче­ская модель объекта исследования. Каким свойствам должна удовлетворять математическая модель?

3. Что является параметром оптимиза­ции, требования, предъявляемые к параметру оптимизации?

4. Что определяет поведение исследуемой сис­темы. Требования, предъявляемые к факторным переменным?

5. В каких точках для предсказания результатов опытов используется нелинейная (квадратичная) модель?

6. Какими методами может осуществляться поиск оптимума по полученному полиному?

7. Как осуществляется поиск оптимума методом нелинейного программирования?

8. Для чего приводятся уравнения регрессии к канонической форме?

9. Как проводится анализ уравнений в канонической форме?

10. Какие виды поверхностей отклика существуют и особенности их анализа?

11. Как отыскивается условный экстремум при наличии нескольких поверхностей отклика?

12. В чем сущность метода неопределенных множеств Лагранжа?