Классификация поверхностей

Для того, чтобы ориентироваться во всем многообразии поверхностей, в способах задания и изображения поверхностей, необходимо классифицировать поверхности по общим, наиболее характерным признакам. Практически каждая поверхность может быть образована несколькими способами. Однако наиболее целесообразным способом образования поверхностей является кинематический, основанный на определенных законах движения. Такой подход к рассмотрению поверхностей позволяет выполнить их классификацию и, что не менее важно, выбрать наиболее рациональную технологию их воссоздания в металле или в другом материале.

Рассмотрим аппарат получения поверхностей (рис. 95).

Введём обозначения:

– S – центр (точка относительно которой перемещается образующая);

– g – от слова genero (образую, порождаю);

– d – от слова dirigo (направляю).

Идея кинематического способа образования поверхностей состоит в том, что линия g,относительно центра S, в пространстве перемещается вдоль направляющей d и при движении образует поверхность. Линия может поступательно перемещаться, или вращается, или перемещается по винтовому закону, или, как по перилам, скользит по заданным линиям.

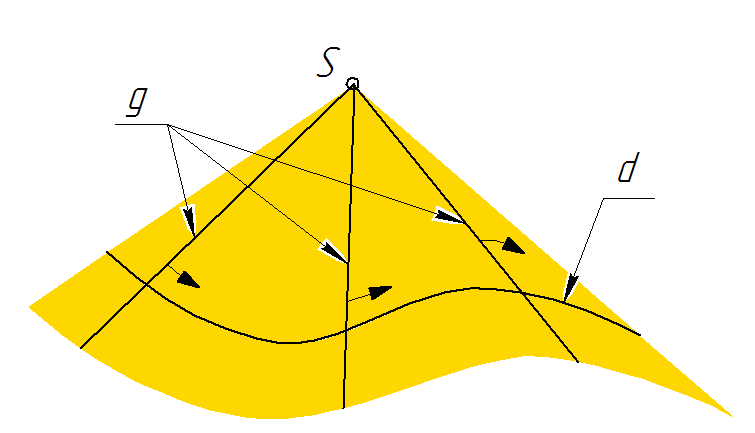
Рис. 95

Линия g называется в этом случае образующей, а множество ее положений в пространстве образует кривую поверхность Ф.

Линии d, по которым скользит образующая g, называются направляющими. Значит, образующие g и направляющие d обязательно пересекаются друг с другом. Очевидно, от формы образующей и характера её изменения зависит класс поверхности.

Если образующая g – прямая линия, то поверхность Ф называется линейчатой.

Если образующая g – кривая линия, то поверхность называется нелинейчатой.

Таким образом, выделено два класса поверхностей – линейчатые и нелинейчатые.

Из наиболее часто встречающихся в технике поверхностей выделены поверхности вращения.

Поверхностью вращения называется поверхность, образованная вращением образующей g вокруг оси вращения.

На рис. 96 изображены линейчатая поверхность вращения (конус), нелинейчатая поверхность вращения (глобоид) и многогранник (пирамида).

При вращении образующей, каждая ееточка описывает окружность с центром S на оси вращения. Эти окружности называются параллелями. Параллель с минимальным размером радиуса называется горлом, а с максимальным размером радиуса – экватором.

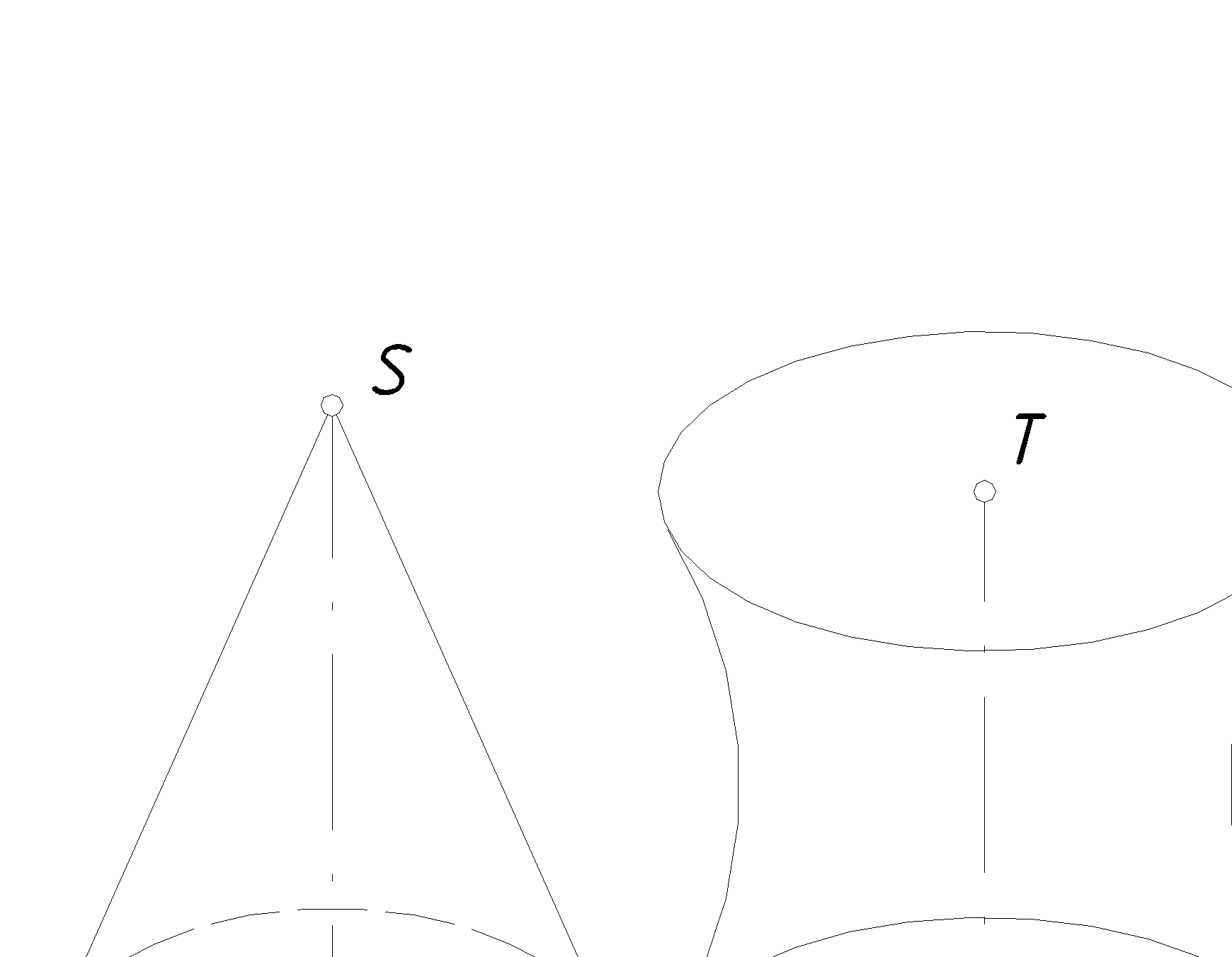
Рис. 96

Кривые, получающиеся в сечении тела вращения плоскостями, проходящими через ось, называются меридианами. Меридиан, параллельный фронтальной плоскости проекций, называется главным.

При вращении кривой 2-го порядка вокруг её оси образуется поверхность 2-го порядка:

· окружность вокруг диаметра – сфера,

· эллипс вокруг малой оси – сжатый эллипсоид вращения,

· эллипс вокруг большой оси – вытянутый эллипсоид вращения,

· парабола вокруг оси – параболоид вращения,

· гипербола вокруг мнимой оси – однополостный гиперболоид вращения,

· гипербола вокруг действительной оси – двуполостный гиперболоид вращения.

Если вращать вокруг оси прямолинейную образующую (прямую), то возможны 3 вида поверхностей:

· если g пересекает ось вращения – коническая поверхность вращения,

· если g параллельна оси вращения – цилиндрическая поверхность вращения,

· если g скрещивается с осью вращения – однополостный гиперболоид вращения.