Лекция 11. ПОВЕРХНОСТИ

11.1. Многогранники.

11.2. Задание многогранника на эпюре Монжа.

11.3. Классификация поверхностей.

11.3. Задание поверхностей вращения на эпюре Монжа.

11.4. Контрольные вопросы.

Многогранники

Отдельным классом поверхностей выделены многогранники. Многогранной поверхностью называется поверхность, образованная частями пересекающихся плоскостей. Если плоскости при этом замыкают пространство со всех сторон, то они образуют многогранник. Говоря другими словами многогранниками это тела, ограниченные плоскими п-угольниками называемыми гранями.

Из всего многообразия многогранников наибольший практический интерес представляют пирамиды, призмы и правильные многоугольники.

Пирамида – это многогранник, одна грань которого многоугольник, а остальные грани треугольники с общей вершиной – рис. 90а.

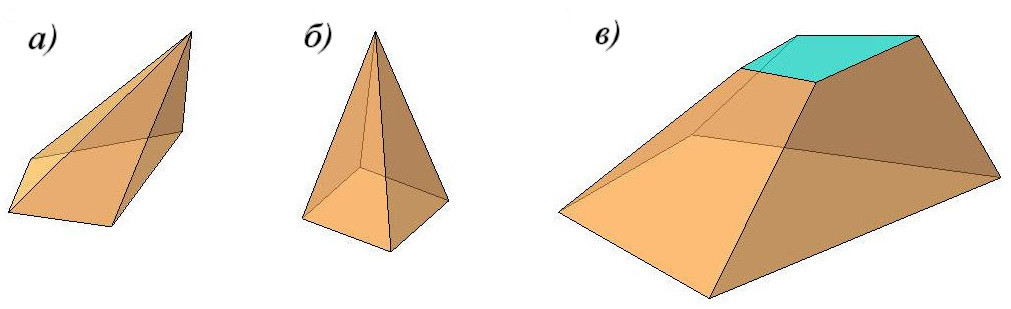
Рис. 90

Пирамиду называют правильной, если основанием ее является правильный многоугольник и высота пирамиды (перпендикуляр, опущенный из вершины на основание) проходит через центр этого многоугольника – рис. 90б.

Пирамида называется усеченной, если вершина ее отсекается плоскостью, пересекающей все ребра, исходящие из этой вершины – рис. 90в.

Призмой называют многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы – рис. 91а.

Призму называют прямой, если ребра ее перпендикулярны плоскости основания – рис. 91б. Если основанием призмы является прямоугольник, призму называют параллелепипедом – рис. 91в.

Правильные многоугольники. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильным. Углы при вершинах такого многогранника равны между собой. Более двух тысяч летназад древнегреческий философ Платон описал все 5 видов правильных многогранников. Поэтому эти многогранники называют телами Платона.

Рис. 91

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (рис. 92а). Это и правильная треугольная пирамида. Каждая из четырех граней тетраэдра может быть выбрана в качестве её основания. Перпендикуляр, опущенный из любой вершины тетраэдра на противолежащую грань, проходит через ее центр.

Октаэдр – правильный восьмигранник (рис. 92б). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины. Каждая из диагональных плоскостей делит октаэдр на две пирамиды с основаниями в виде квадрата.

Гексаэдр – правильный шестигранник (рис. 92в). Это куб, состоящий из шести равных квадратов.

Додекаэдр– правильный двенадцатигранник состоит из 12 правильных и равных пятиугольников, соединенных по три около каждой вершины. Два противолежащих пятиугольника можно принять за основания додекаэдра.

Икосаэдр – состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.

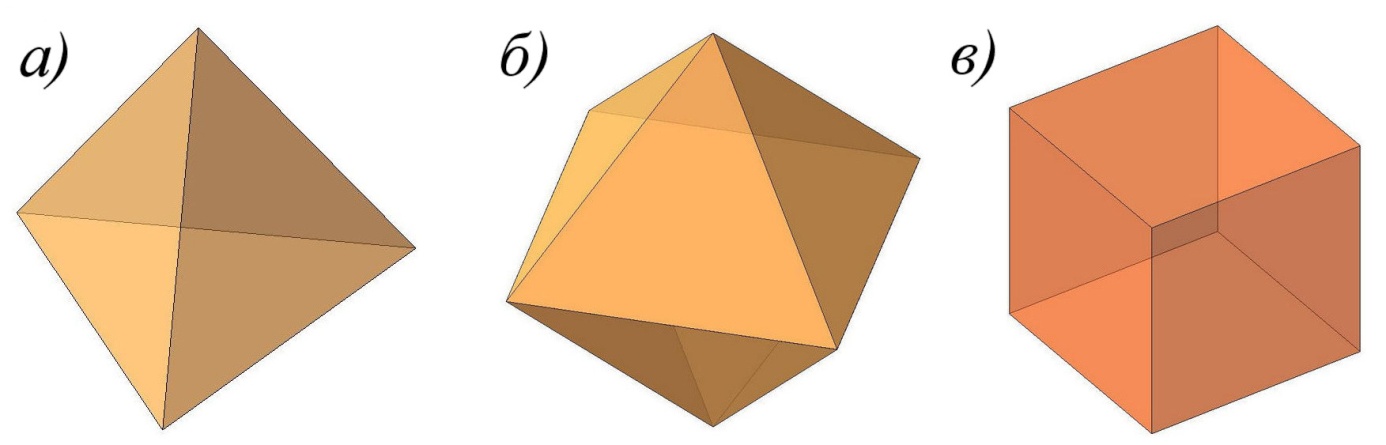
Рис. 92

Леонард Эйлер (1707-1783 гг.) открыл и доказал знаменитую теорему, связывающую числа граней (Г),вершин (В) и ребер (Р) любого выпуклого многогранника: Г + В–Р = 2. Здесь число 2 называют числом Эйлера.