Задание поверхностей вращения на эпюре Монжа

Поверхность на эпюре задается очерком. Очерк поверхности – это линия, разграничивающая проекцию фигуры от остального пространства чертежа. Для построения очерка необходимо построить крайние граничные очерковые образующие. Очерковые образующие лежат в плоскости, параллельной плоскости проекций.

На рис. 97 приведены примеры изображения некоторых тал вращения на эпюре Монжа: прямой круговой конус (рис. 97а); наклонный круговой конус (рис. 97б); прямой круговой цилиндр (рис. 97в); наклонный круговой цилиндр (рис. 97г).

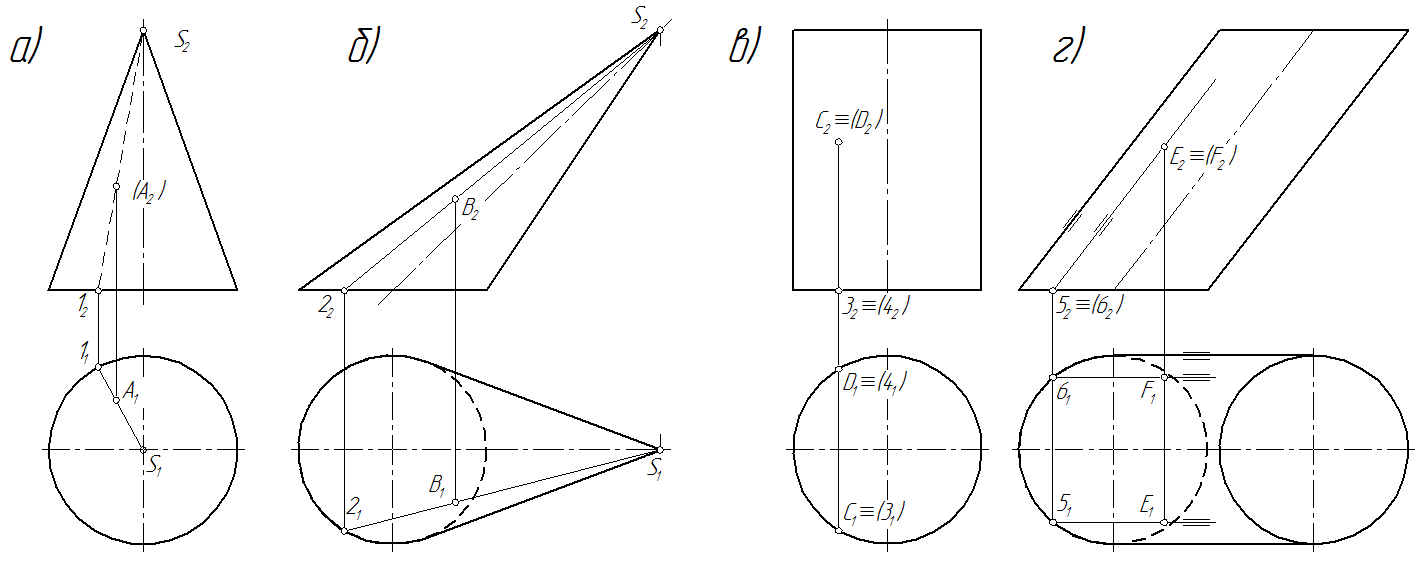
Рис. 87

Если очерки для тела вращения (кроме сферы) называются в зависимости от плоскости проекций на которую оно спроецировано (горизонтальная, фронтальная и профильная), то для сферы (рис. 98) эти очерки носят специфические названия (по аналогии с глобусом):

– очерк на π₂ – главный (нулевой) меридиан;

– очерк на π₁ – экватор;

– очерк на π₃ – профильный меридиан.

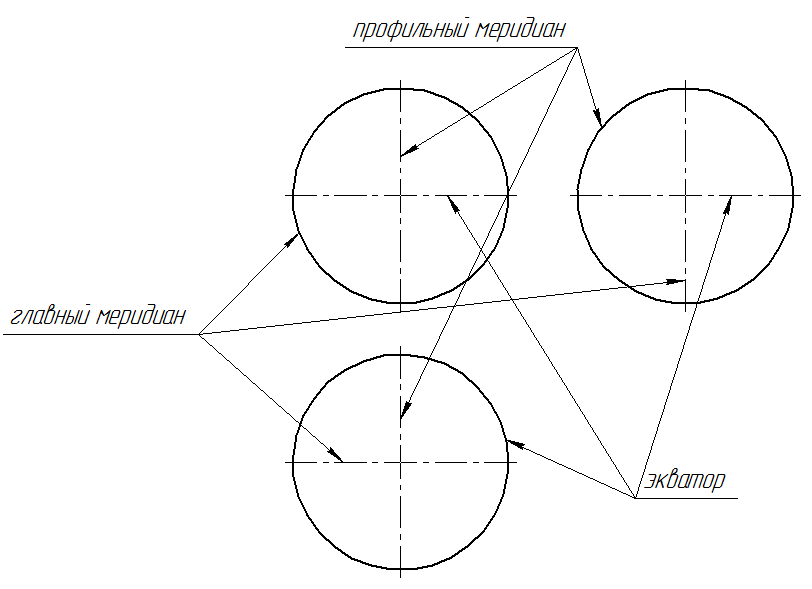
Рис. 98

Для построения точек на поверхностях используются образующие, проходящие через эти точки.

На рис. 97а задана проекция точки (А₂), т.е. точка А располагается на невидимой стороне прямого кругового конуса относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции проводится образующая S-1, на горизонтальной проекции которой и лежит А₁.

На рис. 97б задана проекция В₁ точки В, лежащей на видимой стороне наклонного кругового конуса относительно горизонтальной плоскости проекций. Для нахождения фронтальной проекции проводится образующая S-2, на фронтальной проекции которой и лежит В₂.

У прямого кругового цилиндра (рис. 97в) боковая поверхность занимает горизонтально-проецирующее положение, поэтому горизонтальные проекции С₁ и D₁ определяются с помощью вертикальных линий связи на следе боковой поверхности.

На рис. 97г заданы проекции Е₂ и (F₂) точек Е и F расположенных соответственно на видимой и невидимой сторонах наклонного цилиндра относительно фронтальной плоскости проекций. Для нахождения горизонтальных проекций проводятся образующие, параллельные очерковым боковой поверхности на которых находятся горизонтальные проекции этих точек Е₁ и F₁.

Для нахождения точек на поверхности сферы используют дополнительные широты и удаления от оси вращения.

На рис. 99 задана проекция G₂ точки G, лежащей ниже экватора на видимой стороне сферы относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции: вначале строится дополнительная широта, проходящая через заданную точку, а затем по инварианту принадлежности определяется горизонтальная проекция точки (G₁).

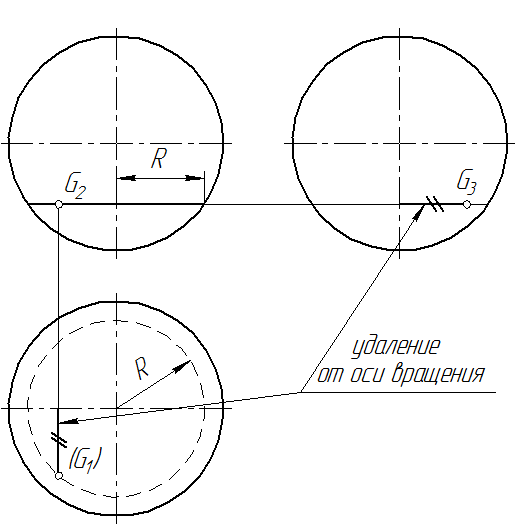
Рис. 99

Следует отметить, что проекция точки на горизонтальной плоскости проекций не видима, т.к. точка G располагается ниже экватора.

Профильная проекция точки G₃ определяется по горизонтальной линии связи и удалению от оси вращения (см. рис. 99). Проекция G₃ видима потому, что фронтальная проекция точки G₂ находится правей фронтальной проекции профильного меридиана.

Контрольные вопросы

1. Как образуются многогранники?

2. Перечислите основные элементы многогранников.

3. Перечислите основные виды многогранников.

4. Как изображаются многогранники на эпюре?

5. Как определяются точки на поверхности многогранника?

6. Перечислите элементы аппарата получения поверхностей.

7. Как образуются поверхности вращения?

8. Как изображаются поверхности на эпюру?

9. Как называются очерки сферы на эпюре?

10. Как определяются точки и линии на поверхностях?