Построение сечения проецирующей плоскостью

При пересечении поверхности плоскостью получается плоская фигура, которая ограничивается линией сечения. Построение сечения заключается в построении этой линии по отдельным точкам.

Каждая точка сечения есть результат пересечения плоскости с какой-либо линией, принадлежащей поверхности. Точки линии сечения подразделяются на опорные и промежуточные.

Опорнымиточками являются точки, лежащие на ребрах и сторонах основания многогранника, точки, лежащие на очерковых линиях поверхности, на линиях основания. К ним же относят точки, определяющие границы видимости сечения, а также высшая и низшая точки сечения. Если линия сечения этими точками полностью не определяется, то строятся промежуточные (между опорными) точки.

От типа линии на поверхности (прямая, окружность или кривая общего вида) зависит уровень сложности построения сечения. Обычно, чем проще эти линии, тем легче построения сечения. Из рис. 104 видно, что:

а) для многогранника достаточно определить точки пересечения ребер и сторон основания с секущей плоскостью (F=SA∩γ, D=SC∩γ, E=SB∩γ);

б) для линейчатой поверхности вращения строятся точки пересечения или прямолинейные образующие, или параллели с секущей плоскостью – например A=S1∩α;

в) для нелинейчатой поверхности вращения строятся точки пересечения параллелей поверхности с секущей плоскостью – например параллель радиуса R пересекается с плоскостью b в точках E и F.

Варианты построения сечения. Если плоскость проецирующая, то все, что принадлежит этой плоскости, проецируется на след-носитель этой плоскости. Значит, одна из проекций фигуры сечения поверхности такой плоскостью имеется на следе-носителе.

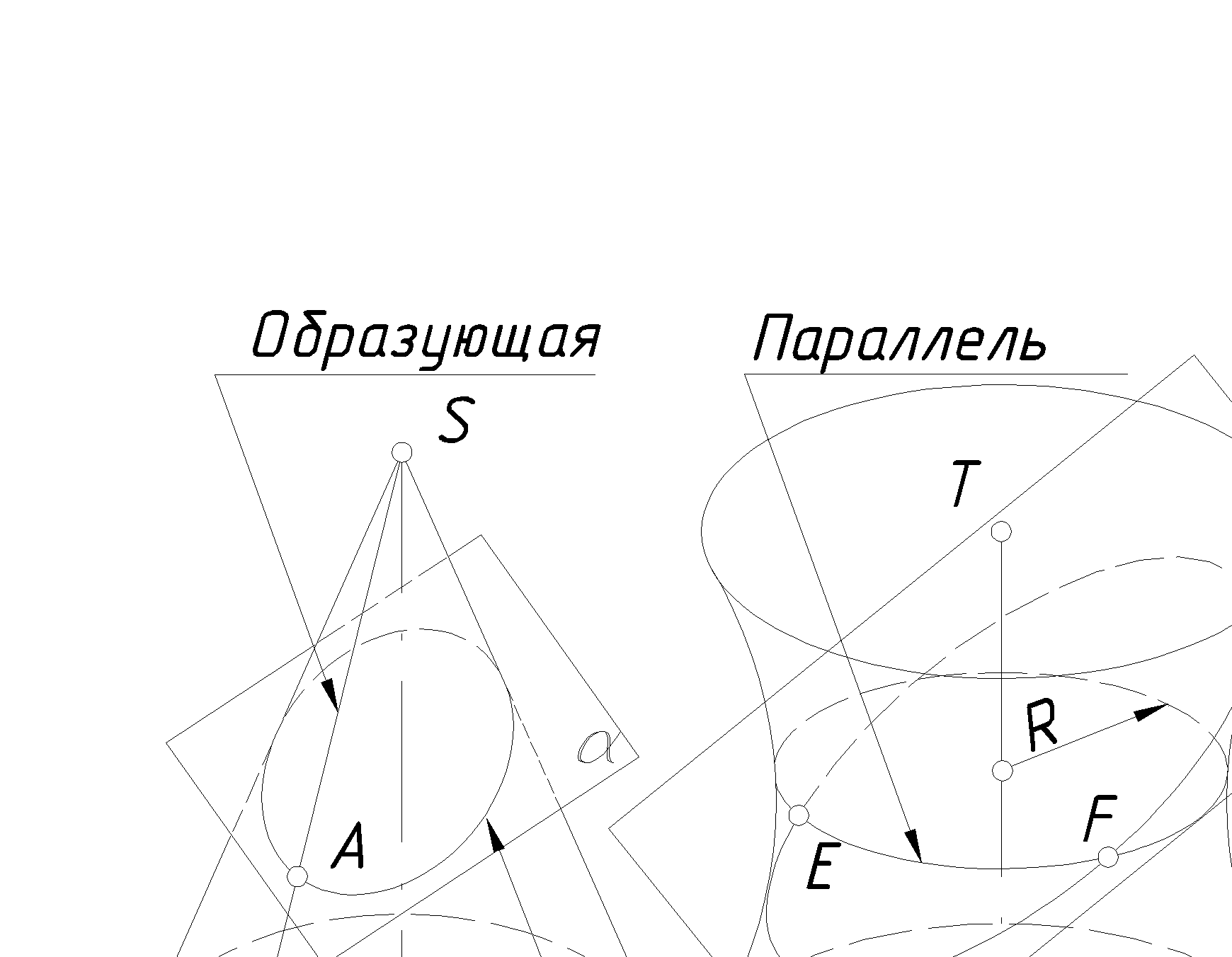
Рис. 104

Вторая проекция сечения строится из условия принадлежности точек сечения или ребрам и сторонам оснований многогранника (пирамида), или прямолинейным образующим линейчатой поверхности (конус), или параллелям нелинейчатой поверхности вращения (часть открытого тора).

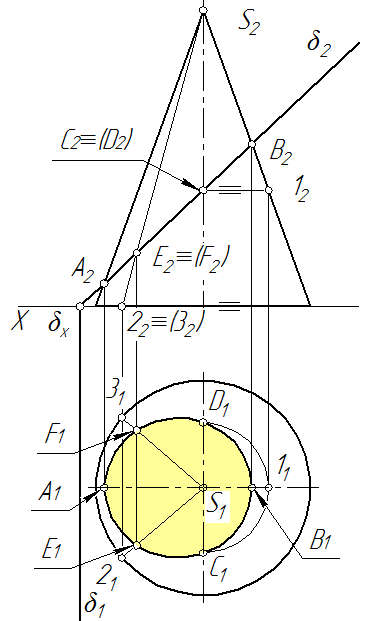
Выполним, для примера, построение фигуры сечения конуса фронтально-проецирующей плоскостью δ – рис. 105.

Так как секущая плоскость фронтально-проецирующая, то, следовательно, фронтальная проекция линии сечение конуса совпадает с фронтальной проекцией плоскости.

Для построения недостающей горизонтальной проекции линии сечения назначаются фронтальные проекции опорных точек (точек, принадлежащих очерковым конуса): А₂, В₂, С₂, D₂. Так как этих точек недостаточно для точного построения горизонтальной проекции сечения, то необходимо назначить не менее трех промежуточных точек между каждыми опорными точками. На примере (рис. 105), с целью чтобы не затенять логику построения сечения, рассматриваются только две промежуточные точки: E₂, F₂.

Построение горизонтальных проекций почек.

Опорные точки. Горизонтальные проекции точек А₁ и В₁ определяются непосредственно по вертикальным линиям связи по принадлежности их очерковым. А горизонтальные проекции точек С₁ и D₁ с использованием подобия линии основания с параллельной линией, проходящей через точки С и D.

Промежуточные точки. Горизонтальные проекции точек Е₁ и F₁ определяются по принадлежности их образующим S-2 и S-3 соответственно.

По полученным горизонтальным проекциям опорных и промежуточных точек строится горизонтальная проекция сечения конуса фронтально-проецирующей плоскостью.