Пересечение многогранника с поверхностью второго рода

В этом случае линией пересечения будет пространственная ломаная, состоящая из дуг кривых, по которым поверхность второго рода пересекается с плоскостями граней. Точки излома будут принадлежать ребрам многогранника.

Рассмотрим порядок построения линии пересечения на примере пересечения конуса с трехгранной призмой (рис. 110).

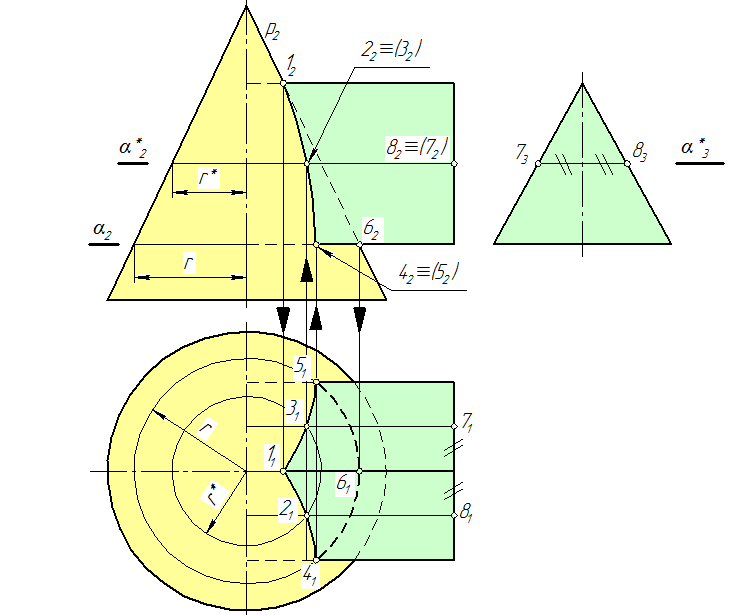
Рис. 110

Решение данной задачи заключается в нахождении точек встречи ребер многогранника с поверхностью конуса. Для этого в качестве плоскости-посредника целесообразно использовать плоскость уровня а.

Определение точек излома. Здесь следует отметить, что точку встречи ребра т с поверхностью конуса можно определить как общую точку двух пересекающихся прямых, т.е. ребра т и образующей р(m₂∩p₂)=l₂→l₁, l₃. Для получения других точек излома воспользуемся плоскостью-посредником α, которую проведем через грань, образованную ребрами k и п. Линией сечения конуса будет окружность радиуса r. Точки пересечения 4 и 5 этой окружности и ребер k и п являются точками излома линии пересечения поверхностей λ и μ, т.е. k₁∩b₁=5₁→5₂ и n₁∩b₁=4₁→4₂.

Определение точек дуг. Здесь следует обратить внимание на то, что дуга между точками излома 4 и 5на плоскости проекций совпадет с линией сечения конуса с плоскостью-посредником а, т.к. плоскость а≡(k∩n).

Положения промежуточных точек для других дуг, например, 2 и 3, определяются как точки пересечения линий сечений поверхностей плоскостью-посредником а^*.

После определения необходимого количества точек наносят линию пересечения поверхностей с учетом ее видимости. Для нанесения дуг целесо­образно использовать лекало. Видимость линии пересечения определяется с помощью конкурирующих точек.

Контрольные вопросы.

1. Как строят линию пересечения двух поверхностей?

2. Какова типа линия пересечения двух многогранников?

3. Алгоритм определения линии пересечения двух многогранников.

4. В чём сущность способа вспомогательных секущих плоскостей при построении линии пересечения двух поверхностей?

5. Какие точки являются опорными и промежуточными при построении линии пересечения многогранника с телом вращения?

6. Каков алгоритм решения задач на определение линии пересечения многогранника с телом вращения?

7. Как определяется видимость поверхностей относительно друг друга?