Способ вспомогательных сфер
Способ вспомогательных сфер применяется для построения линии пересечения поверхностей тел вращения, имеющих пересекающиеся оси. Кроме того, оси этих тел параллельны одной из плоскостей проекций т.е. образуют плоскость уровня.
В основе этого способа применяется поверхность посредник в виде сферы с использованием теоремы Монжа (см. п14.2 и рис. 112).
Рассмотрим построение линии пересечения на примере конуса и цилиндра (рис. 114).
Выберем центр вспомогательных сфер в точке пересечения осей заданных поверхностей (точка О).
Опорные точки 1 и 2на очерковых образующих, расположенные в одной плоскости, определяются непосредственно. Линия пересечения заключается между этими точками. Одна из них определяет максимальный радиус вспомогательных сфер Rmax = O212 (наиболее удаленная фронтальная проекция от точки пересечения осей О2). Минимальный радиус Rminберется наибольшим радиусом сферы, которую можно вписать в одну из заданных поверхностей, при этом пересекая другую поверхность.
Для построения промежуточных точек проводят несколько вспомогательных сфер (Rmin<R<Rmax). Эти сферы пересекают заданные поверхности по окружностям b и п. Окружности b и п, пересекаясь, дают дополнительные точки линии пересечения 3 и 4, проекции которых определяются вначале на π2 (b2∩п2=32 и b2∩п2=42), а затем на плоскости π1 как точки окружностей радиусами r.
Полученные точки (опорные и промежуточные) последовательно соединяют на фронтальной и горизонтальной проекциях.
На фронтальной проекции видна ближняя часть кривой (12-42-22) и не видна дальняя (12-32-22). Кривая пересечения поверхностей симметрична, значит (12-42-22)≡(12-32-22). На горизонтальной проекции видна часть кривой (... -31-11-41– ...), проекции точек которой расположены выше фронтальной проекции оси симметрии наклонного цилиндра. В этом случае границей видимости линии пересечения на горизонтальной проекции служат точки на горизонтальных проекциях очерковых образующих наклонного цилиндра.
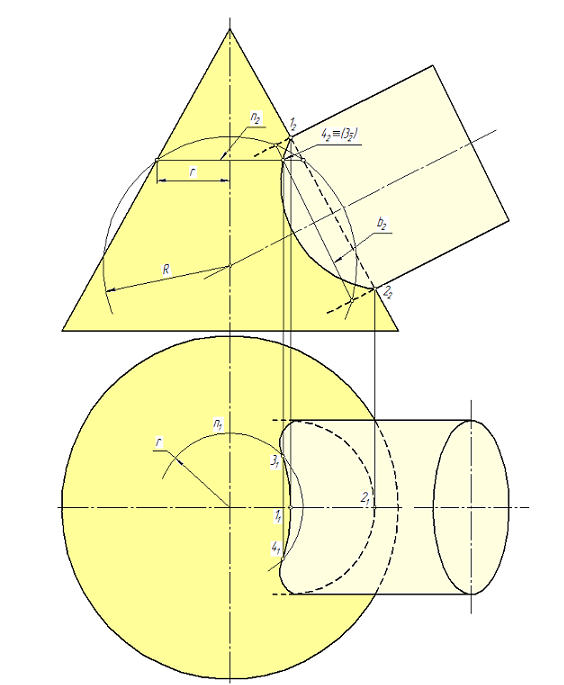
Рис. 114
Контрольные вопросы.
1. В чём сущность способа вспомогательных секущих плоскостей при построении линии пересечения двух тел вращения?
2. Каков принцип построения линии пересечения двух поверхностей вращения, оси которых параллельны или пересекаются (скрещиваются) под прямым углом?
3. По каким линиям пересекаются соосные поверхности?
4. В чём суть теоремы Монжа?
5. Перечислите частные случаи пересечения тел вращения.
6. Покажите как для частных случаев изображаются линии пересечения тел вращения на эпюре.
7. В каких случаях удобно применять метод секущих сфер?
8. Каков принцип построения линии пересечения двух поверхностей методом секущих сфер?
Дата добавления: 2017-09-19; просмотров: 276;
