Развертка конической поверхности общего вида

Рассмотрим развертку конической поверхности на примере построения развертки наклонного конуса (рис. 118).

Для получения развертки боковой поверхности наклонного конуса в него вписывают многогранную пирамиду. Следует отметить, что чем больше граней у вспомогательной пирамиды, тем точнее развертка.

Примечание. Рекомендуется окружность основания конуса делить на 12 равных частей при R>25 мм и на 8 – при R<25 мм (R – радиус круга основания конуса).

Развертывание конической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной пирамиды (см. п.10.2). На рис. 102, чтобы не затенять ход решения, в конус вписывается шестигранная пирамида с правильным шестиугольником в основании. Определение натуральных величин боковых ребер S2 и S3 осуществляется способом вращения вокруг оси i перпендикулярной плоскости π₁. Боковые ребра S1 и S4 на π₂ проецируются без искажения так как они являются фронталями, а основание на π₁ так как оно является горизонтальной плоскостью уровня.

Отличительной особенностью при построении является то, что полученные точки боковой поверхности, описывающие окружность основания конуса, соединяются не прямыми, а кривой с помощью лекало.

Основание конуса на развертке изображается кругом (в натуральную величину), касающимся в любой точке кривой боковой поверхности, описывающей основание.

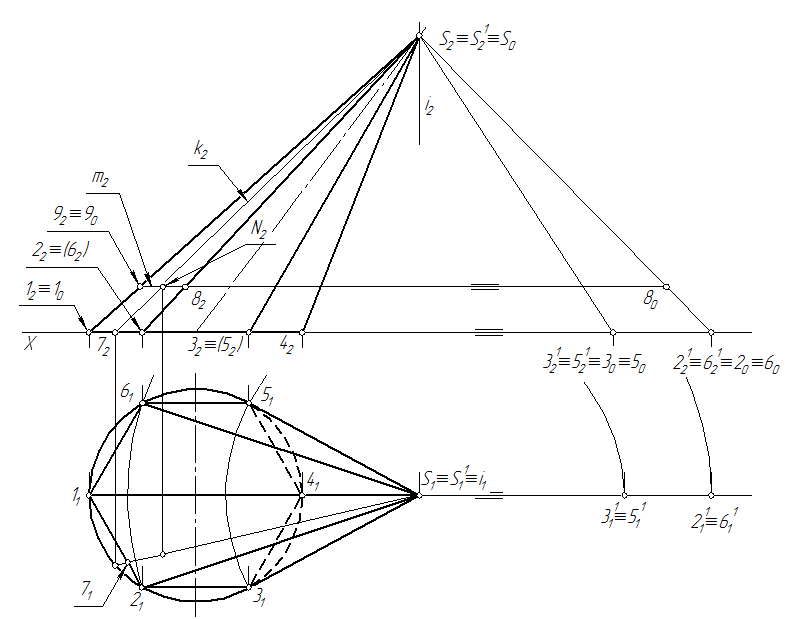
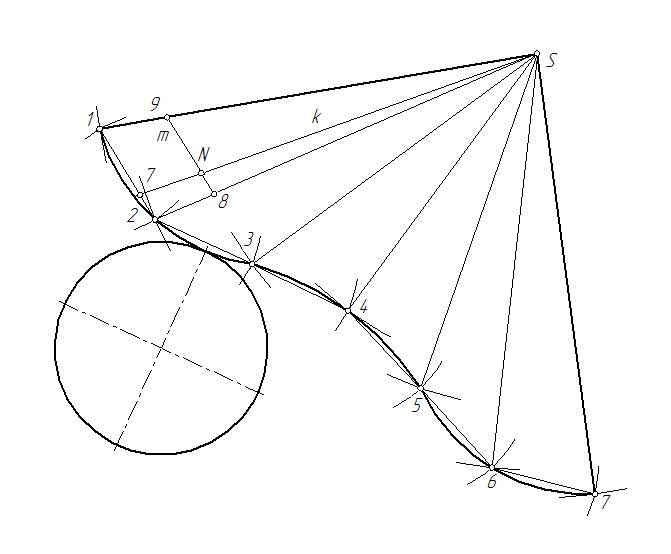
Рис. 118

Нанесение линии на развертку производится по точкам. Количество точек зависит от сложности конфигурации линии. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁ и k₂, образующей k,проходящей через вершину S и данную точку. Затем прямую k наносят на развертку при условии, что [17]=[1₁7₁]. Далее, через точку N проводится вторая прямая m, параллельная плоскости π₁. Эта прямая пересекает ребра S1 и S2 соответственно в точках 9 и 8. Точка 9 на развертке определяется используя отрезок, а точка 8 – используя отрезок [2₀8₀]=[18]. Положение точки 8₀ на ребре S₀2₀ находится с использованием теоремы Фалеса. Точка N на развертке определяется пересечением прямых k и m.

Контрольные вопросы

1. Что называется развёрткой поверхности?

2. Какие поверхности относятся к развёртывающимся поверхностям?

3. Можно ли построить развёртку неразвёртывающейся поверхности?

4. Каким способом строят развёртки пирамидальных (конических) поверхностей? В чём его сущность?

5. Как нанести на развёртку пирамидальной (конической) поверхности точку, ей принадлежащую?

6. В чем заключается сущность метода раскатки при развертывании призмы?

7. В чем заключается сущность метода нормального сечения при развертывании призмы?

8. Как нанести на развёртку призматической (цилиндрической) поверхности точку, ей принадлежащую?