Прямоугольная диметрическая проекция

Аксонометрические изображения, построенные в прямоугольной димет­рии, обладают наилучшей наглядностью, однако построение изображений сложнее, чем в изометрии. Расположение аксонометрических осей в диметрии следующее: ось OZ направлена вертикально, а оси OХ и OY составляют с горизонтальной линией, проведённой через начало координат (точка О), углы, соответственно, 7º10´ и 41º25´ (см. треугольник штриховок рис. 128).

Рис. 128

Положение осей можно также определить, отложив от начала координат в обе стороны по восемь равных отрезков; через восьмые деления проводят вниз линии и на левой вертикали откладывают один отрезок, а на правой – по семь отрезков. Соединив полученные точки с началом координат, определяют направление осей ОХ и ОУ (рис. 128).

Коэффициенты искажения по осям ОХ, OZ равны 0,94, а по оси ОY – 0,47. Для упрощения в практике пользуются приведёнными коэффициентами искажения: по осям OX и OZ коэффициент равен 1, по оси ОY – 0,5.

Построение аксонометрических проекций предмета осуществляется по характерным точкам, дугам и окружностям.

Для построения аксонометрической проекции точки (рис. 129) требуется определить длины звеньев ее аксонометрической координатной ломаной. Для изометрической проекции длины звеньев этой ломаной равны длинам соответствующих звеньев натуральной координатной ломаной. Длины звеньев, параллельных осям ОХ, OY и OZ аксонометрической координатной ломаной для точки берутся равными длинам соответствующих звеньев натуральной ломаной (x_A, y_A/2, z_A).

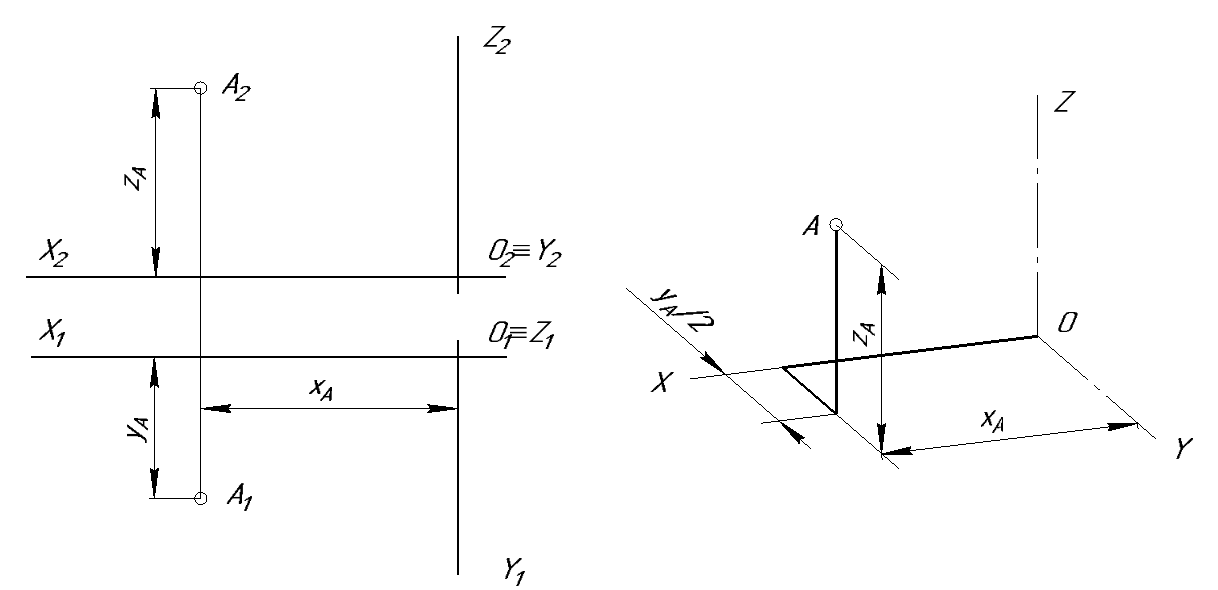
Рис. 129

Окружности в прямоугольной диметрии изображаются в виде овалов ориентированных относительно осей. Построение прямоугольной диметрии куба с окружностями, вписанными в три видимые его грани показано на рис. 130. Окружности, вписанные в грани, представляют собой эллипсы двух видов. Оси эллипса, расположенного в грани, которая параллельна координатной плоскости XOZ, равны: большая ось – 1,06 D; малая – 0,94 D, где D – диаметр окружности, вписанной в грань куба. В двух других эллипсах большие оси равны 1,06 D, а малые – 0,35 D.

Для упрощения построений можно заменить эллипсы овалами. На рис. 131 даны приёмы построения четырехцентровых овалов, заменяющих эллипсы.

Овал в передней грани куба (ромба) строится следующим образом. Из середины каждой стороны ромба (рис. 131а) проводят перпендикуляры до пересечения с диагоналями. Полученные точки 1-2-3-4 будут являться центрами сопрягающих дуг. Точки сопряжений дуг находятся посредине сторон ромба. Построение можно выполнить и другим способом. Из середин вертикальных сторон (точки N и M) проводят горизонтальные прямые линии до пересечения с диагоналями ромба. Точки пересечения будут искомыми центрами. Из центров 4 и 2 проводят дуги радиусом R, а из центров 3 и 1 – радиусом R₁.

Рис. 130

Овал, заменяющий два других эллипса, выполняют следующим образом (рис. 131б). Прямые LP и MN, проведенные через середины противоположных сторон параллелограмма, пересекаются в точке S. Через точку S проводят горизонтальную и вертикальную линии. Прямую LN, соединяющую середины смежных сторон параллелограмма, делят пополам, и через ее середину проводят перпендикуляр до пересечения его с вертикальной линией в точке 1.

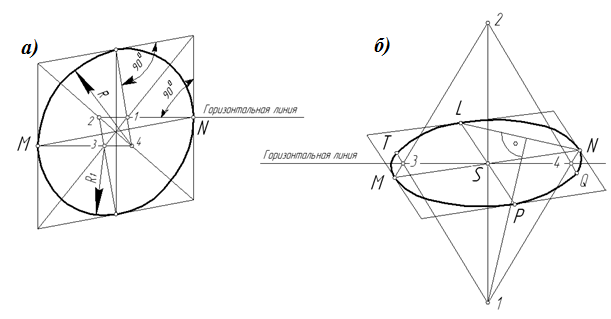
Рис. 131

на вертикальной прямой откладывают отрезок S-2 = S-1. Прямые 2-М и 1-N пересекают горизонтальную прямую в точках 3 и 4. Полученные точки 1, 2, 3 и 4 будут центрами овала. Прямые 1-3 и 2-4 определяют точки сопряжения T и Q.

из центров 1 и 2 описывают дуги окружностей TLN и QPM, а из центров 3 и 4 – дуги MT и NQ.