Частные случаи разверток

К частным случаям разверток относятся развертки прямого кругового конуса и прямого кругового цилиндра.

Развертка прямого кругового конуса.Развертка прямого кругового конуса (рис. 119) представляет собой сектор круга, радиус которого равен длине образующей конуса b, а центральный угол а

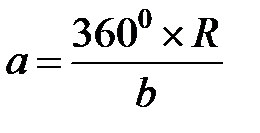, (1)

где R – радиус основания конуса.

Нанесение линии на развертку производится по точкам с использованием лекал. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁и k₂ образующей k, которой принадлежит эта точка. Затем прямую k наносят на развертку при условии, что длина дуги A₀K₀ равна длине дуги A₁K₁. Далее, используя теорему Фалеса, определяют истинное положение точки N₀: ([K₀N₀] =m).

Примечание. Развертку прямого конуса можно строить как развертку конической поверхности общего вида, т.е. в конус необходимо вписать правильную многогранную пирамиду.

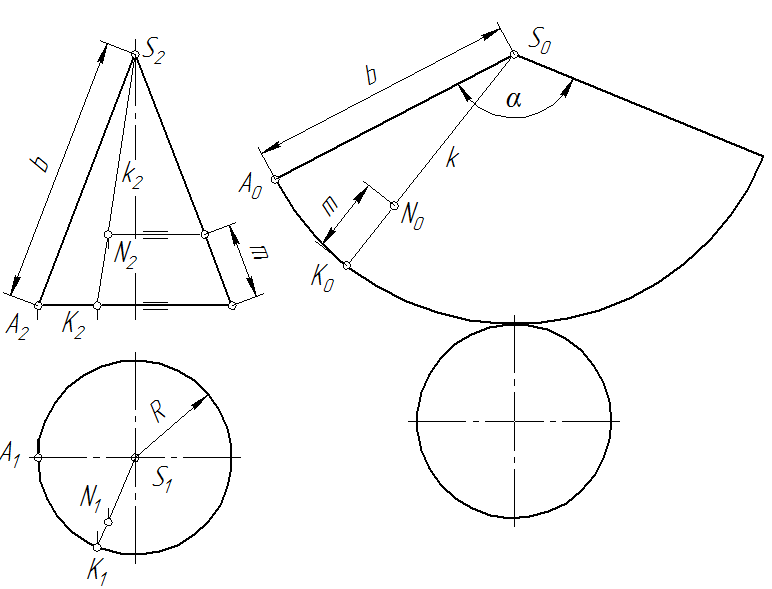
Рис. 119

Методика построения линии пересечения поверхностей на развертке конуса аналогична методике, используемой при развертке пирамиды.

Развертка прямого цилиндра.Развертка боковой поверхности прямого цилиндра представляет собой прямоугольник (рис. 120), одна сторона которого равна образующей l, а другая – длине окружности основания n:

n=2πR, (2)

где R – радиус основания окружности.

Каждое основание цилиндра наносят в виде круга с радиусом R,ка­сающегося в любой точке стороны п прямоугольника, описывающего его.

Нанесение линии пересечения поверхностей на развертку производится по точкам с использованием лекал. Положение любой точки поверхности на развертке, например N, определяется следующим образом. Вначале находят проекции k₁ и k₂ образующей k, которой принадлежит точка N. Затем определяют положение этой образующей на развертке по условию, что отрезок [B₀K₀] равен длине дуги B₁K₁. Так как k₂=k, то положение точки N₀на развертке определяется как [N₀K₂]= [N₂K₂].

Примечание. Развертку прямого цилиндра можно строить как развертку наклонного цилиндра, т.е. в цилиндр необходимо вписать правильную многогранную призму.

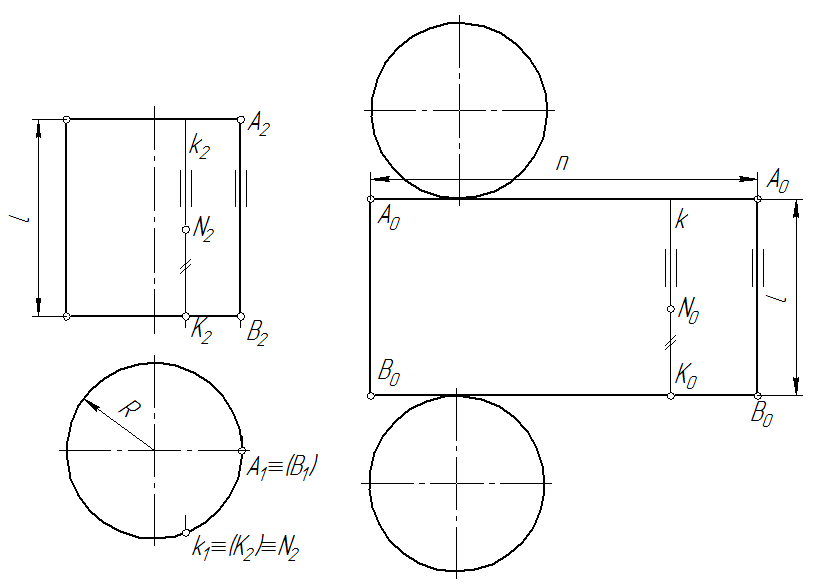
Рис. 120

Развертка сферы

Сферическая поверхность является неразвертываемой. Здесь можно говорить только об условном развертывании. На рис. 121 показан один из приемов построения. Поверхность “разрезают” несколькими плоскостями, проходящими через ось сферы, перпендикулярную π₁. Точность развертки зависит от числа плоскостей – чем больше плоскостей, тем точнее развертка. На рис. 104 число таких плоскостей 12 (фронтальные проекции линий пересечения не показаны).

Дуги окружностей на плоскости π₁ в лепестках развертки заменяют прямыми, касательными к этим дугам, например, прямая А₁В₁ заменяет дугу ав.

На плоскости π₂ дугу 1₂7₂делят на равные части: 1₂2₂=2₂3₂=...=6₂7₂ (чем больше частей – тем точнее развертка). Принимая точки 1₂ 2₂, 3₂,... за фронтальные проекции отрезков АВ, CD, EF,образующих лепестки развертки, строят их горизонтальные проекции A₁B₁,C₁D₁, E₁F₁,...

На прямой l откладывают отрезок A₀B₀= A₁B₁ и через его середину (точка 1₀) проводят перпендикуляр k. На этом перпендикуляре откладывают отрезки [1₀2₀]= 1₂2₂, [2₀3₀]= 2₂3₂, [3₀4₀]= 3₂4₂, [4₀5₀]= 4₂5₂, [5₂6₂]= 5₂6₂и[6₂7₂]= 6₂7₂и через полученные точки 2₀, 3₀, 4₀, 5₀,и6₀проводят отрезки [C₀D₀]=[C₁D₁]_, [E₀F₀]=[E₁F₁] и т.д., параллельные прямой A₀B₀, при этом точки 2₁≡2₀,3₁≡3₀ и т.д.

По лекало через полученные точки А₀, D₀, F₀,...,7₀ и В₀ С₀, E₀…, 7₀ проводят кривые. В результате получается приближенная развертка половины лепестка сферической поверхности. Далее, используя эту часть лепестка, строят недостающую часть развертки.

Рис. 121

Примечания.

1. Окружность сферы рекомендуется делить на 12 равных частей (лепестков) при R>25 мм и на 8 – при R<25 мм (R – радиус сферы).

2. Дугу 1₂7₂ следует делить не менее чем на 4 равные части (6, 8, 10 или 12 частей).

Построение линии пересечения поверхностей на развертке произво­дится по ее точкам с использованием лекал.

Для нахождения положения точки на развертке, например, S, опреде­ляют ее положение относительно экватора ( 1₂S*₂) и центральной линии сегмента [S₁N₁], в котором она находится. Далее полученные значения этих величин наносят на развертку, т.е. [1N]- 1₂S₂* и [SN]=[S₁N₁].

Контрольные вопросы

1. Какую форму имеет развёртка поверхности прямого кругового конуса?

2. Как нанести на развёртку прямого кругового конуса точку, ей принадлежащую?

3. Какую форму имеет развёртка поверхности прямого кругового цилиндра?

4. Как нанести на развёртку прямого кругового цилиндра точку, ей принадлежащую?

5. Каким способом сроят развёртки наклонных цилиндрических поверхностей?

6. Как нанести на развёртку наклонной цилиндрической поверхности точку, ей принадлежащую?

7. Каким способом строят развертку сферы?

8. Как нанести на развёртку сферы точку, ей принадлежащую?