Лекция 15. РАЗВЕРТКИ

15.1. Общие сведения.

15.2. Развертка пирамиды.

15.3. Развертка призмы.

15.4. Развертка конической поверхности общего вида.

15.5. Контрольные вопросы.

Общие сведения

Разверткой поверхности называется плоская фигура, полученная в результате совмещения поверхности с плоскостью. Построение разверток поверхностей имеет большое практическое применение при изготовлении различных изделий из листового материала. Это обшивка самолётов и судов, всевозможные резервуары и трубопроводы в нефтехимической и газовой промышленности, изделия швейной и кожевенной промышленности и т.д.

Для построения развёртки используются ортогональные проекции по­верхности. Связь между ними описывается инвариантным свойством со­хранения площадей соответствующих фигур. Это свойство влечёт за собой ещё такие свойства:

– длины соответствующих линий поверхности и её развёртки равны;

– углы, образованные линиями поверхности, равны углам, состав­ленным их образами на развёртке;

– прямая поверхности отображается на прямую развёртки;

– параллельные прямые поверхности отображаются на параллельные прямые развёртки.

Разработка наиболее простых и точных способов построения разверток необходима для изготовления тонкостенных изделий заданной формы и размеров. Чем рациональнее и точнее способ выполнения разверток и их раскроя, тем экономичнее технология изготовления изделий. При этом экономятся листовой материал и рабочее время.

Теоретически точно развертываются поверхности многогранников, прямых круговых конусов и цилиндров. Приближенными развертками являются развертки поверхностей наклонных конусов и цилиндров, а развертки сфер относятся к условным.

В общем случае, построение любой развертки сводится к построению натуральной величины и формы элементов, составляющих поверхность.

Развертка пирамиды

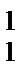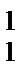Развертка пирамиды относится к точным разверткам. Ее получения катет S B равен основывается на способе построения треугольника по трем известным сторонам, где в качестве сторон треугольника используются натуральные величины ребер пирамиды.

Поэтому для построения развертки пирамиды (рис. 115) необходимо найти натуральные величины ее боковых ребер и основания.

Основание пирамиды представляет собой треугольник, изображенный в натуральную величину на плоскости π₁, так как является горизонтальной плоскостью уровня.

Для определения натуральных величин боковых ребер воспользуемся способом прямоугольного треугольника (см. п 5.1). Так в треугольнике ∆S₀S 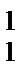B 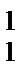горизонтальной проекции ребра S₁B₁, а катет S₀S 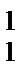– разности координат по оси 0Z его концов. Следовательно, гипотенуза S₀B 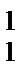, этого треугольника, есть натуральная величина ребра SB. Аналогично находятся и другие натуральные величины ребер.

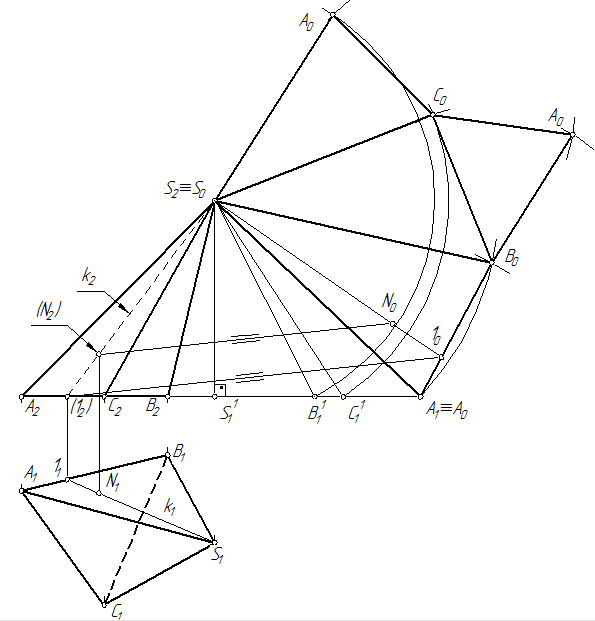
Рис. 115

После определения натуральных величин ребер строится развертка боковой поверхности пирамиды. Для этого на любом из ребер, например, S₀A₀ (или отдельно), последовательно строятся треугольники каждой грани по трем известным их сторонам: ∆S₀A₀B₀ → ∆S₀B₀C₀ → ∆S₀C₀A₀. Следует помнить, что построение боковых граней заканчивается тем же ребром, с которого начинается построение развертки боковой поверхности пирамиды. После построения боковой поверхность пирамиды к любому ребру основания пирамиды пристраивается ее основание.

Нанесение линии на развертку производится по точкам. Количество точек зависит от сложности конфигурации линии. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁ и k₂, прямой k,проходящей через вершину S и данную точку. Затем прямую k наносят на развертку при условии, что [А₀1₀]=[А₁1₁]. Далее, используя теорему Фалеса, определяется истинное положение точки N₀ на развертке.

Развертка призмы

Развертка призмы может осуществляется несколькими способами, одними из которых являются способ раскатки и способ нормального сечения.

Способ раскатки. В общем случае каждая грань призмы (рис. 116) имеет форму параллелограмма. В данном примере натуральные величины ребер определяется на плоскости π₂, а оснований – на плоскости π₁.

Если в исходных данных призма занимает общее положение, то необходимо способами преобразования эпюра преобразовать его проекции так, чтобы грани призмы были либо фронталями, либо горизонталями, а плоскости оснований – плоскостями уровней.

Развертка боковой поверхности осуществляется совмещением граней призмы с плоскостью проекций. Для этого все точки вращают в плоскостях, перпендикулярных проекциям ребер, а расстояния между ребрами берутся равными соответственно величинам сторон основания.

Рассмотрим на примере (рис. 100). За начало развертки принимается одна из фронтальных проекций ребра (на примере – С₀Е₀=С₂Е₂). Из проекции вершины F₂ проводится перпендикуляр к фронтольной проекции ребра B₂F₂. Принимая вершину Е₀ за центр окружности делается засечка на перпендикуляре радиусом равным E₁F₁. Полученная засечка является вершиной параллелограмма F₀. Используя вершину F₀, ребро С₀Е₀и принцип параллельности достраивается параллелограмм E₀C₀B₀F₀. Далее аналогично строится грани A₀B₀F₀D₀ и A₀D₀E₀C₀.

После построения развертки боковой поверхности к ней пристраиваются основания.

Нанесение линии на развертку производится точкам. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁ и k₂ прямой k,которая параллельна боковым ребрам призмы и которой принадлежит эта точка. Затем прямую k наносят на развертку при условии, что [A₀K₀]=[A₁K₁].Далее, используя [K₂N₂]=[K₀N₀], определяют истинное положение точки N₀.

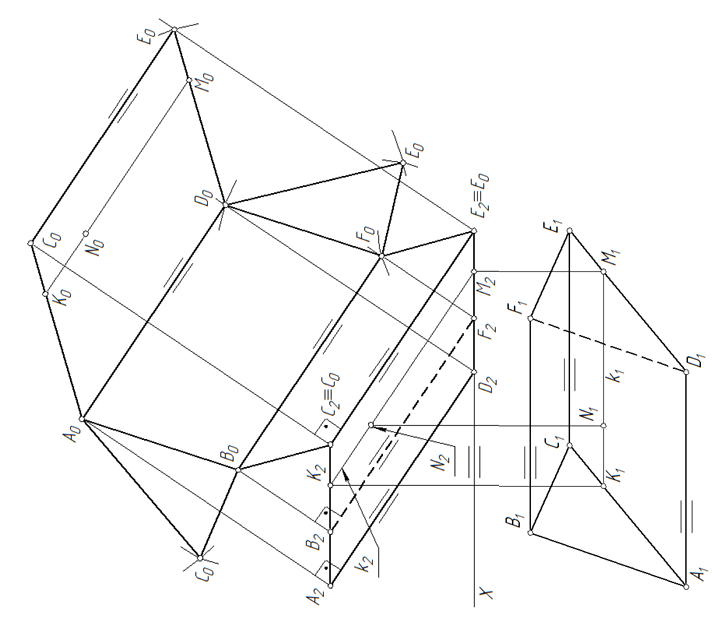
Рис. 116

Способ нормального сечения. Сущность данного способа построения развертки призмы заключается в следующем.

Заданную призму пересекается плоскостью, перпендикулярной боковым рёбрам, и строится проекция и натуральная величина сечения призмы этой плоскостью (нормальное сечение). Также определяются натуральные величины отрезков боковых рёбер призмы, лежащих выше и ниже нормального сечения.

На рис. 117 показано:

– натуральная величина нормального сечения (∆1₄2₄3₄) призмы АВСDEF, полученное сечением ее фронтально-проецирующей плоскостью α с использованием способа замены плоскостей проекций;

– натуральные величины ребер и их деления секущей плоскостью определяется на плоскости π₂;

– натуральные величины оснований определяются на плоскости π₁.

Для построения развертки на свободном поле эпюра проводится горизонтальная линия и на ней от произвольной точки откладываются друг за другом стороны нормального сечения призмы: [1-2]→[2-3]→[3-1].

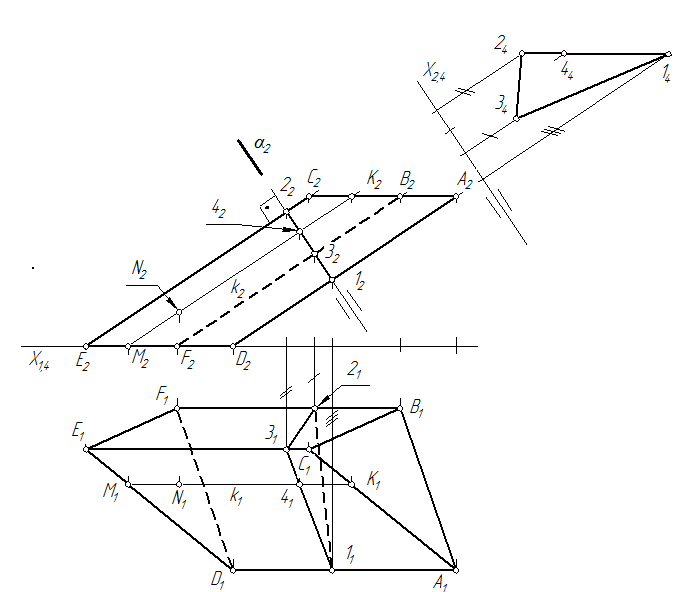
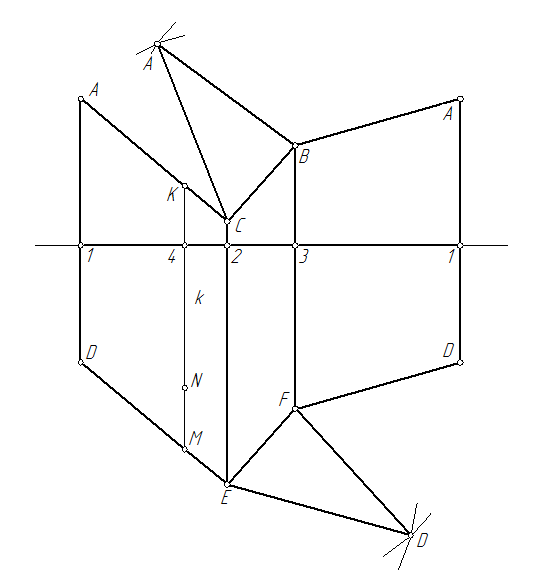
Рис. 117

Через полученные точки 1, 2, и 3 проводятся вертикальные прямые линии, на которых вниз откладываются натуральные величины отрезков боковых рёбер призмы, лежащих ниже нормального сечения, а вверх – натуральные величины отрезков боковых рёбер призмы, лежащих выше нормального сечения. Соединяя построенные точки между собой отрезками прямых, получается развертка боковой поверхности призмы. Достроив к ней натуральные величины верхнего и нижнего оснований, получается полная развертка поверхности призмы.

Нанесение линии на развертку производится точкам. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁ и k₂ прямой k,которая параллельна боковым ребрам призмы и которой принадлежит эта точка. Эта прямая пересекает нормальное сечение в точке 4. Используя проекцию 4₄ на натуральной величине нормального сечения, а также натуральную величину отрезка 4N определяется положение точки N на развертке.