Теорема Монжа. Частные случаи

Теорема Монжа. Если тела вращения имеют одну общую ось, то линия их взаимного пересечения будет представлять собой окружность.

Если общая ось вращения параллельна одной из плоскостей проекций, то на эту плоскость проекций линия пересечения тел проецируется в виде прямой.

Если общая ось вращения перпендикулярна плоскости проекций, то на эту плоскость линия пересечения проецируется в виде окружности (в натуральную величину).

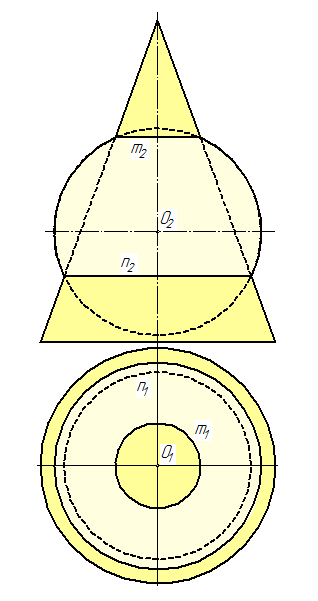
Геометрическая интерпретация этого положения показана на примере пересечения прямого кругового конуса и сферы, которые имеют общую ось вращения (рис. 112). Т.к. эти тела вращения имеют общею ось вращения следовательно линии пересечения этих тел m и n являются окружностями. Учитывая что общая ось вращения этих тел параллельна фронтальной плоскости проекций и перпендикулярно горизонтальной плоскости проекций, значит линии перенесения проецируются на π₂ в виде прямых m₂ и n₂, а на π₁ в виде окружностей m₁ и n₁.

Частные случаи. Если у двух поверхностей (рис. 113) вращения оси пересекаются и вспомогательная сфера, взятая с центром в точке пересечения этих осей, касается одновременно поверхностей двух заданных тел, то линия их взаимного пересечения распадется на две плоские кривые линии — эллипсы

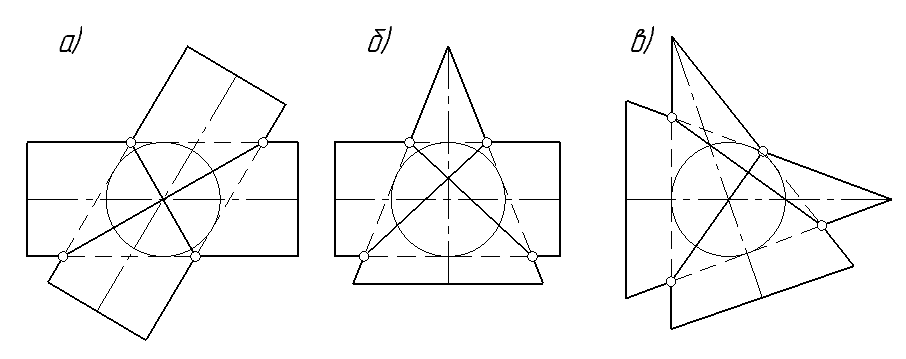
Рис. 113

В ортогональных проекциях пересекающиеся оси двух заданных тел должны быть расположены параллельно какой-либо плоскости проекций, тогда линия их пересечения спроецируется как две пересекающиеся прямые.

На рис. 113 оси двух заданных тел располагаются параллельно фронтальной плоскости проекций. В зависимости от формы поверхности геометрических тел и их взаимного расположения линия пересечения может распасться на два эллипса одинаковой величины (рис. 113б).