Лекция 12. ПОВЕРХНОСТИ

12.1. Виды сечений.

12.2. Построение сечения проецирующей плоскостью.

12.3. Пересечение прямой с поверхностью.

12.4. Контрольные вопросы.

Виды сечений

Вид сечения поверхности зависит от типа поверхности и положения секущей плоскости относительно поверхности.

Независимо от расположения секущей плоскости, сечением многогранника будет многоугольник, вершинами которого будет является точки пересечения секущей плоскости с ребрами многогранника (рис. 100).

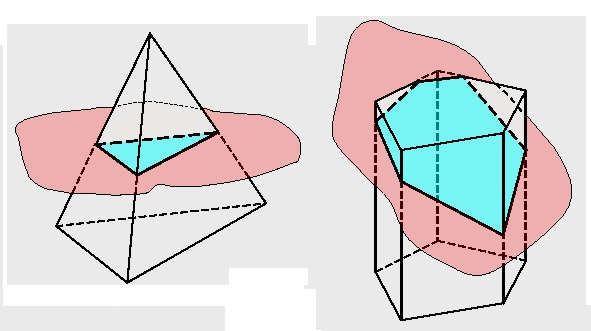
Рис. 100

Сечением цилиндра является круг если секущая плоскость перпендикулярна оси вращения (рис. 101а), овал (элепс) если секущая плоскость не перпендикулярна и не параллельна оси вращения (рис. 101б) или прямоугольник если секущая плоскость параллельна оси вращения (рис. 101в).

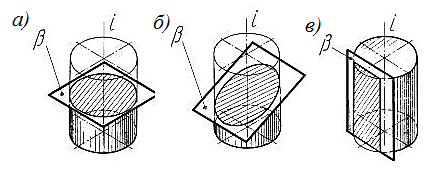
Рис. 101

Сечением сферы всегда является круг (рис. 102).

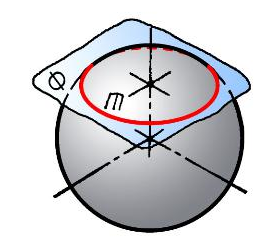
Рис. 102

Рассмотрим более подробней сечение конуса. Поверхность конуса вращения определяется уравнением 2-го порядка значит, и сечением конуса могут быть кривые 2-го порядка, т.е. окружность, эллипс, парабола или гипербола.

В начертательной геометрии тип кривой 2-го порядка может быть определен следующим образом.

Если секущая плоскость параллельна двум образующим конуса, то сечением будет гипербола. Обе ветви гиперболы можно получить, если конус будет иметь две полы. На рис. 103 плоскость А-А проходит параллельно двум образующим конуса (S-1 и S-2) и поэтому пересекает конус по гиперболе. Слева изображена истинная величина сечения А-А и 3-мерное изображение конуса с сечением А-А.

Если секущая плоскость параллельна одной образующей конуса, то сечением будет парабола. На рис 103 плоскость Б-Б проходит параллельно правой очерковой образующей S-3 конуса, поэтому сечением является парабола, истинная величина которой показана справа с сопровождающей надписью Б-Б. Ещё правее и ниже дано 3-мерное изображение конуса, усеченного плоскостью Б-Б.

Если секущая плоскость пересекает все образующие, то сечением будет эллипс. Плоскость В-В пересекает все образующие верхней полы конуса. Значит, сечением будет являться эллипс. Истинная величина сечения размещена справа с надписью В-В. Ещё правее и чуть выше показана 3-мерная модель конуса, усечённого плоскостью В-В.

Если секущая плоскость перпендикулярна к оси вращения конуса, то сечением будет окружность. На рис. 103 основания конуса перпендикулярны оси конуса OS и поэтому являются окружностями, горизонтальные проекции которых совпадают.

Если секущая плоскость проходит через вершину S конуса и пересекает его, то понятно, что в сечении будут треугольники (образующие конуса и линия сечения основания). Если секущая плоскость проходит через S и не пересекает образующие, сечением будет точка S. На рис. 29 сечения от плоскости b А-А, Б-Б, В-В и построены в натуральную величину и размещены в проекционной связи с секущей плоскостью.

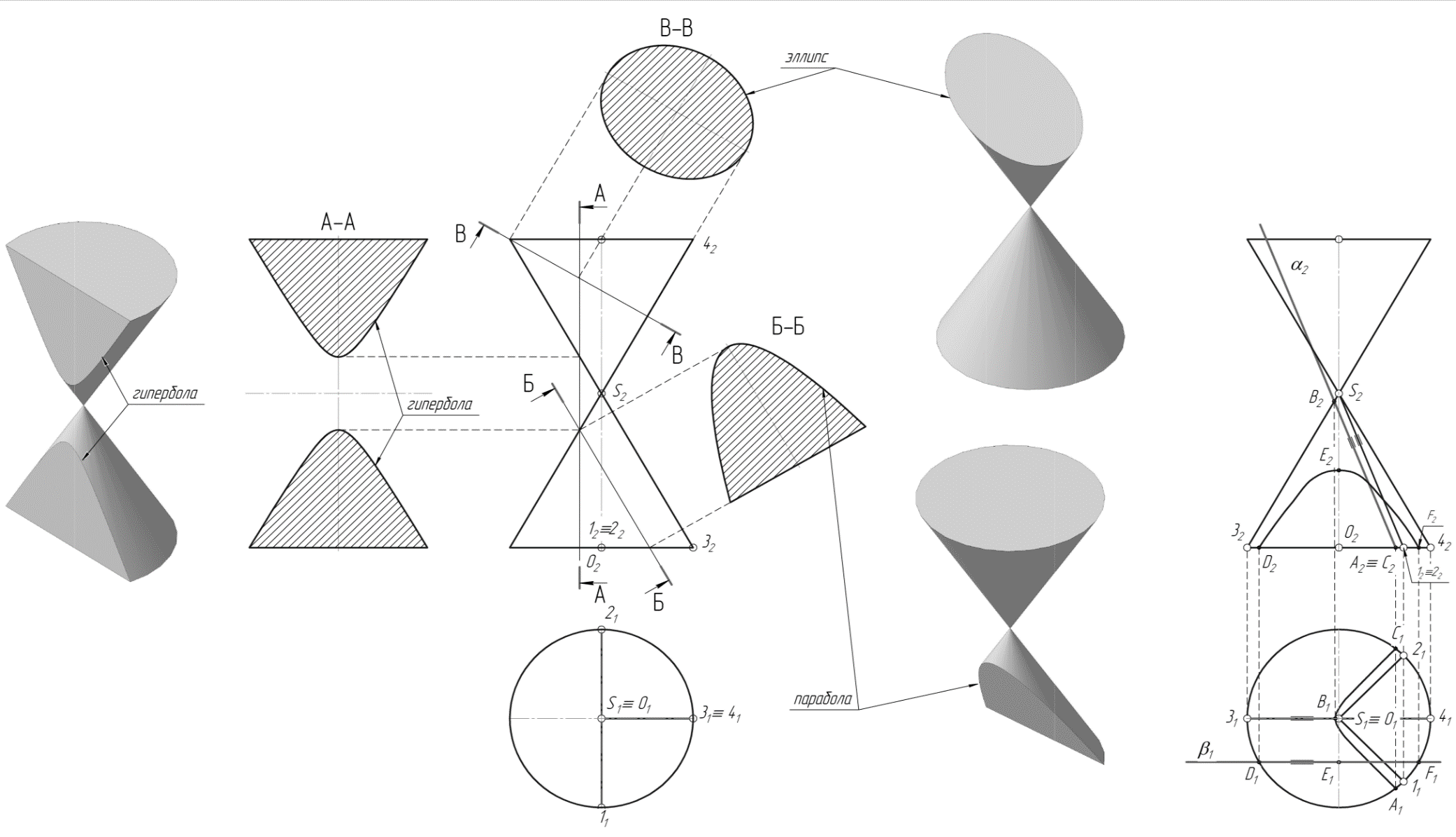
Рис. 29

На правой части рис. 103 изображены фронтальная и горизонтальная проекции того же конуса. Но здесь показаны приёмы получения в сечении гиперболы. Для этого через фронтальную проекцию S₂ вершины S под любым углом проводим проекции образующих S-1 и S-2 конуса, лежащих во фронтально проецирующей плоскости. Затем параллельно плоскости этих образующих проводим фронтальный след a₂ плоскости a сечения. Строим горизонтальную проекцию гиперболы, опорными точками которой являются точки А, С и вершина В. Понятно, что эта проекция гиперболы не определяет истинной величины сечения.

Ещё один вариант построения сечения в виде гиперболы получается, если секущая плоскость b будет параллельна фронтальной плоскости проекций, так как в этом случае плоскость b параллельна двум образующим – S-3, S-4. Фронтальная проекция гиперболы (D и F – опорные точки сечения, а E – вершина гиперболы) есть истинная величина сечения.