Задание многогранников на эпюре Монжа
Как видно из рис. 93, каждый многогранник содержит грани, ребра и вершины. Их совокупность называется сеткой. На эпюре многогранники изображаются проекциями своей сетки – рис. 94. Каждая вершина имеет своё обозначение. Ребра многогранников есть линии пересечения смежных граней. Каждая грань – это часть плоскости, ограниченной ребрами и сторонами основания многогранника.
Рассмотрим, в каком случае точка пространства будет принадлежать многограннику.
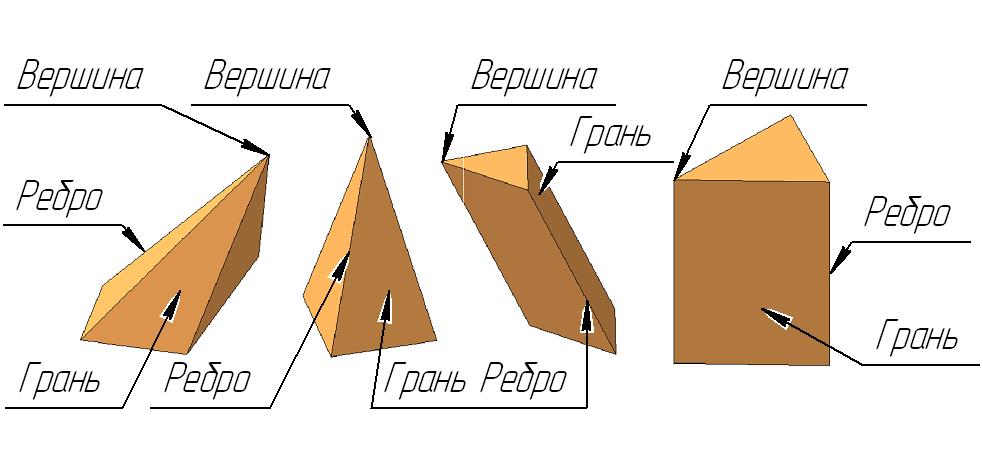
Рис. 93
Понятно, что точка пространства может принадлежать: вершине многогранника, его ребру или грани многогранника.
В первом и втором варианте проблем изображения точки на чертеже многограннике нет.
Если же точка принадлежит грани многогранника, т.е. плоскости, надо пользоваться информацией: точка лежит в плоскости, если она лежит на прямой этой плоскости.
Условимся записывать обозначение точки, лежащей на невидимой для наблюдателя грани, в скобках, например, (E2).
На рис. 94а задана проекция (E2), т.е. точка E располагается грани ADS четырёхгранной пирамиды, невидимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится прямая S-1 в грани BCS через вершину S, на горизонтальной проекции которой и лежит E1.
На рис. 94б задана проекция F2, т.е. точка F располагается на грани BCS правильной четырёхгранной пирамиды, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится в грани BCS прямая, параллельная стороне AD основанияпирамиды. На горизонтальной проекции этой прямой и лежит F1.
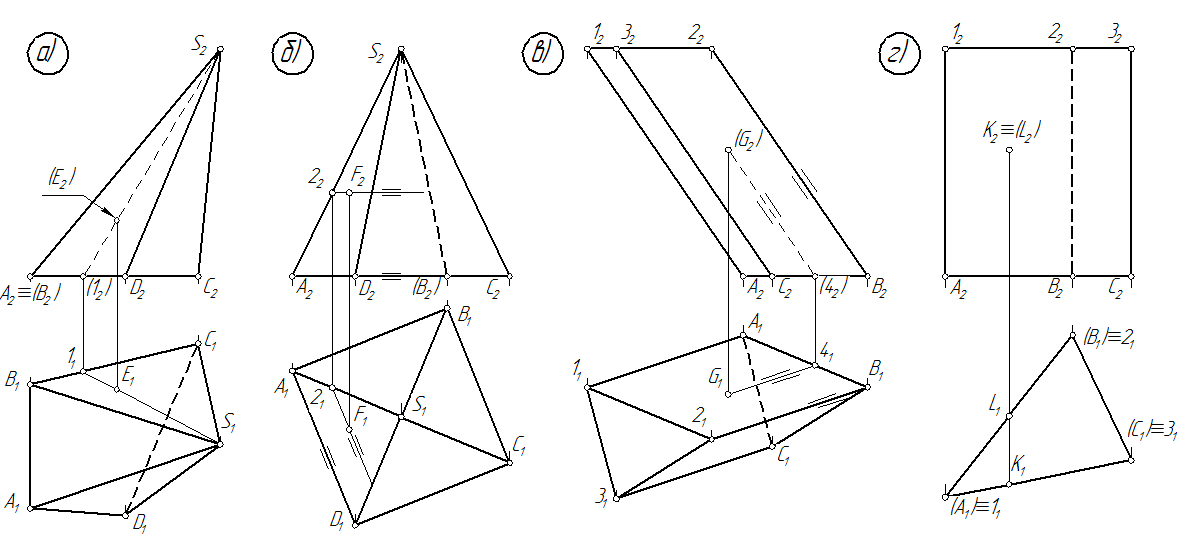
Рис. 94
На рис. 94в задана проекция (G2), т.е. точка G располагается на грани
1-2-BA наклонной призмы, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проведена в грани
1-2-BA прямая, параллельная ребрам призмы. На горизонтальной проекции этой прямой и лежит G1.
У прямой призмы (рис. 94г) грани занимают горизонтально-проецирующее положение, поэтому горизонтальные проекции K1 и L1 определяются с помощью вертикальных линий связи на следах граней.
Дата добавления: 2017-09-19; просмотров: 454;
