Способ плоско параллельного перемещения

При использовании способа вращения фигур иногда происходит наложение изображений. Этого можно избежать, применяя способ плоскопараллельного перемещения. Этот способ относится к способам третей группы.

Сущность этого способа заключается в том, что все точки геометрической фигуры перемещаются в плоскостях, параллельных одной из плоскостей проекций.

Следовательно, точки движутся в плоскостях уровня, и одна из проекций геометрической фигуры перемещается без изменения формы и размеров, а на другой проекции траектории движения точек параллельны оси 0Х.

Рассмотрим преобразование отрезка АВ прямой общего положения в проецирующую прямую (рис. 89). Первоначально преобразуем прямую АВ во фронталь, переместив проекцию А₁В₁ без изменения размеров параллельно оси 0Х (в произвольном месте). Точки прямой АВ перемещаются параллельно плоскости π₁. На фронтальной проекции траектории точек параллельны оси 0Х. Новые фронтальные проекции отрезка А В определяются на пересечении линий связи от А 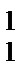В 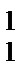с траекториями движения точек.

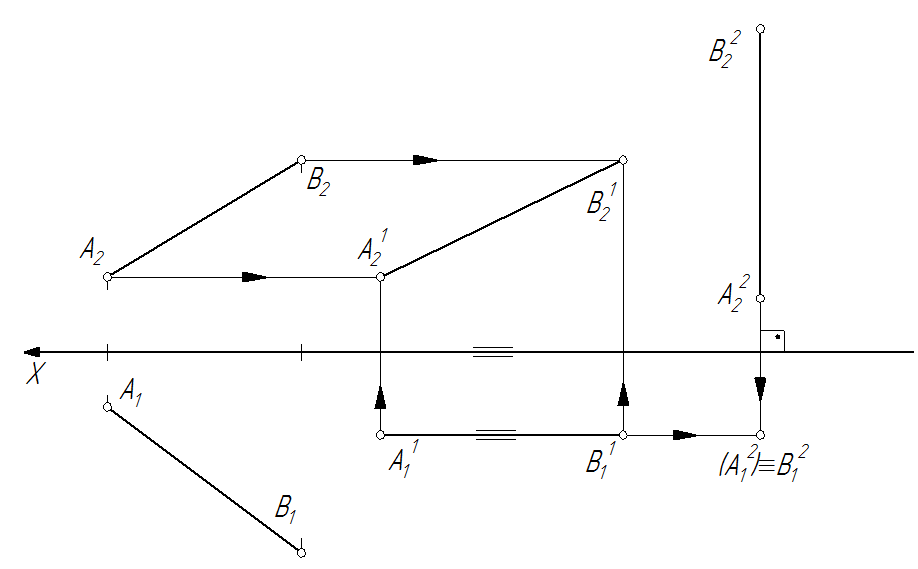
Рис. 89

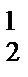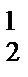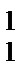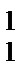Проекция А В является натуральной величиной АВ, так как первым перемещением прямая преобразована во фронталь (характерный признак – А В ∥0Х).

Второе перемещение выполняется параллельно плоскости π₂. Фронтальная проекция перемещается без изменений размеров перпендикулярно оси 0Х (А 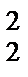В ⊥0Х). На горизонтальной проекции точки движутся параллельно оси 0Х, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

10.3. Определение натуральных величин
геометрических объектов

Определение натуральных величин геометрических объектов базируется на использовании четырех основных задач. К таким параметрам геометрических объектов относятся 15 основных параметров.

1. Определение натуральной величины отрезка.(Задача № 1).

2. Расстояние между двумя точками.Между точками проводится отрезок и решается задача № 1. Натуральная величина отрезка есть искомая величина.

3. Определение угла наклона прямой к плоскости проекций. Решается задача № 1 и используются свойства прямых уровней.

4. Расстояние от точи до прямой. Прямая переводится в проецирующие положение (задача № 2). Расстояние от проекции точки до вырожденной проекции прямой является искомой величиной.

5. Расстояние между скрещивающимися прямыми. Одна из прямых переводится в проецирующие положение (задача №2). Перпендикуляр от вырожденной проекции прямой до проекции другой прямой является искомой величиной.

6. Расстояние между параллельными прямыми. Одна из прямых переводится в проецирующие положение (задача № 2). Расстояние между вырожденными проекциями прямых является искомой величиной.

7. Натуральная величина плоской фигуры. Плоская фигура заключается в плоскость. Затем эта плоскость переводится в положение плоскости уровня (задача № 4). Натуральная величина плоской фигуры определяется по свойству плоскости уровня.

8. Угол между пересекающимися прямыми.Прямые заключаются в плоскость и плоскость переводится в положение уровня (задача № 4). Угол пересечения натуральных величин прямых является искомой величиной.

9. Угол между скрещивающимися прямыми.Используя параллельный перенос одной из прямых, прямые доводят до положения пересечения прямых и задачу решают, как определения угла между пересекающимися прямыми.

10. Угол наклона плоскости к плоскости проекций. Плоскость переводится в проецирующие положение (задача № 3). Угол наклона вырожденной проекции плоскости к оси является искомой величиной.

11. Расстояние от точки до плоскости. Плоскость переводится в проецирующие положение (задача № 3). Перпендикуляр от проекции точки до вырожденной проекции плоскости является искомой величиной.

12. Расстояние от прямой до плоскости, которой она параллельна. Плоскость переводится в проецирующие положение (задача № 3). Перпендикуляр между проекциями прямой и вырожденной проекцией плоскости является искомой величиной.

13. Расстояние между параллельными плоскостями. Одна из плоскостей переводится в проецирующие положение (задача №3). Перпендикуляр между вырожденными проекциями плоскостей является искомой величиной.

14. Определение двугранного угла. Линия пересечения плоскостей переводится в проецирующие положение (задача №2). Угол между вырожденными проекциями плоскостей является искомой величиной.

15. Определение угла наклона прямой к плоскости. Вначале плоскость переводится в плоскость уровня (задача № 4), а затем находится натуральная величина прямой (задача № 1). Угол между натуральной величиной прямой и вырожденной проекцией плоскости является искомой величиной.

Примечание. Если преобразование производится применительно к какому-то одному геометрическому образу, то оно относится ко всему изображению в целом.

Контрольные вопросы

1. Как определяется натуральная величина отрезка способом вращения вокруг проецирующей прямой?

2. Как получить проецирующею прямую способом вращения вокруг проецирующей прямой?

3. Как получить проецирующею плоскость способом вращения вокруг проецирующей прямой?

4. Как получить плоскость уровня способом вращения вокруг проецирующей прямой?

5. В чем заключается сущность способа плоско параллельного перемещения и в каких случаях он применяется?

6. Перечислите основные геометрические характеристики, определяемые способами преобразования чертежа.