Крутое восхождение по поверхности отклика
Градиентом называют вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой [3]. Градиент 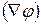 непрерывной однозначной функции
непрерывной однозначной функции 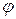 есть вектор:
есть вектор:
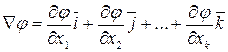 ,
,
где 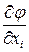 частная производная функции по i-му фактору;
частная производная функции по i-му фактору; 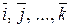 – единичные векторы в направлении осей факторов. Согласно теореме Тейлора о разложении аналитической функции в ряд частные производные функции по факторам равны по величине и знаку соответствующим коэффициентам регрессии. Следовательно, градиент
– единичные векторы в направлении осей факторов. Согласно теореме Тейлора о разложении аналитической функции в ряд частные производные функции по факторам равны по величине и знаку соответствующим коэффициентам регрессии. Следовательно, градиент 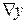 функции отклика у есть вектор:
функции отклика у есть вектор:
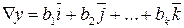 .
.
Движение по градиенту обеспечивает наиболее короткий путь к оптимуму, так как направление градиента – это направление самого крутого склона, ведущего от данной точки к вершине. Если изменять факторы пропорционально их коэффициентам с учетом знака, то движение к оптимуму будет осуществляться по самому крутому пути. Этот процесс движения к области оптимума называют крутым восхождением. Технику расчета крутого восхождения рассмотрим на примере задачи с одним фактором 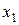 (рис.2.1).
(рис.2.1).
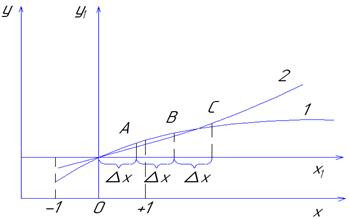
Рис.2.1 Схема к расчету координат точек в направлении градиента:
1 – график неизвестной функции отклика;
2 – прямая 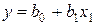 - направление градиента.
- направление градиента.
Предположим, что кривая 1 представляет собой неизвестную функцию отклика. В результате реализации плана эксперимента с центром в точке О получено уравнение регрессии 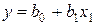 , адекватно описывающее функцию отклика в области значений фактора
, адекватно описывающее функцию отклика в области значений фактора 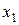 от –1 до +1.
от –1 до +1.
Значение коэффициента регрессии 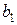 равно тангенсу угла между линией регрессии и осью данного фактора.
равно тангенсу угла между линией регрессии и осью данного фактора.
Если шаг движения по оси 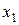 принять равным
принять равным 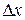 , то, умножив его на
, то, умножив его на 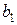 , получим координаты (
, получим координаты ( 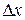 и
и 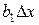 ) точки А, лежащей на градиенте. После второго шага расстояние по оси
) точки А, лежащей на градиенте. После второго шага расстояние по оси 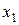 будет равно
будет равно 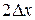 . Умножив
. Умножив 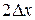 на
на 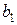 , найдем координаты
, найдем координаты 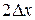 и
и 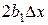 точки В, лежащей на градиенте, и т. д. Затем проводят опыты с условиями, отвечающими точкам на градиенте.
точки В, лежащей на градиенте, и т. д. Затем проводят опыты с условиями, отвечающими точкам на градиенте.
По результатам этих опытов определяют область оптимума. В практических задачах для сокращения объема эксперимента проводят не все, а только часть опытов, предусмотренных крутым восхождением.
Условия опытов выбирают так, чтобы область оптимума можно было заключить в «вилку». После этого опыты проводят в точках интервала, образованного точками «вилки», до нахождения наилучшего результата.
В случае k факторов расчет крутого восхождения по оси каждого фактора производят аналогичным образом, так как коэффициенты 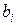 определяются независимо друг от друга. При этом движение по осям всех факторов осуществляют одновременно.
определяются независимо друг от друга. При этом движение по осям всех факторов осуществляют одновременно.
Шаг движения по градиенту выбирают таким, чтобы его минимальная величина была больше ошибки, с которой фиксируют фактор. Максимальную величину шага ограничивает область определения фактора.
Необходимо учитывать, что при движении к оптимуму малый шаг потребует значительного числа опытов, а большой шаг может привести к проскоку области оптимума. Шаг движения выбирают для одного фактора, а для остальных его рассчитывают по выражению
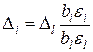 ,
,
где
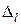 – выбранный шаг движения для фактора
– выбранный шаг движения для фактора
l; 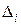 – шаг движения для i-го фактора;
– шаг движения для i-го фактора;
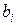 ,
, 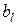 – коэффициенты регрессии i-го и l-го факторов;
– коэффициенты регрессии i-го и l-го факторов;
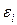 ,
, 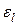 –интервалы варьирования i-го и l-го факторов.
–интервалы варьирования i-го и l-го факторов.
Движение по градиенту должно начинаться от нулевой точки основного уровня каждого фактора, так как коэффициенты регрессии вычислены для функции отклика, разложенной в ряд Тейлора в окрестности нулевой точки.
Если коэффициенты регрессии значительно отличаются друг от друга, то рекомендуют изменить интервалы варьирования факторов и провести новую серию опытов, ибо при различии коэффициентов на порядок и более многофакторный эксперимент при крутом восхождении может превратиться в однофакторный.
Рассчитав шаг движения для каждого фактора, находят условия «мысленных» опытов.
«Мысленными» называют опыты, условия, проведения которых на стадии крутого восхождения установлены с учетом шага движения для каждого фактора. С целью проверки результатов крутого восхождения часть мысленных опытов реализуется.
Если при движении к оптимуму возникает ситуация, препятствующая изменению каких-либо факторов, то эти факторы можно фиксировать на оптимальных уровнях, продолжая движение по остальным факторам.
Крутое восхождение прекращается, если найдены оптимальные условия или если ограничения на факторы делают дальнейшее движение по градиенту неразумным.
Рассмотрим метод Бокса – Уилсона на примере исследования модифицирования чистого алюминия молибденом. В качестве параметра оптимизации y выбрали число зерен алюминия в 1 см2, определяющееся металлографически.
На параметр оптимизации оказывают существенное влияние следующие факторы: х1 – количество введенного в алюминий молибдена, %; х2 – температура, ° С; x3 - время нагрева, мин; х4 – скорость охлаждения., х1х2 x3 – факторы количественные; x4 – фактор качественный, принимающий два значения: быстрое охлаждение в графитовом тигле и медленное охлаждение в шамотном тигле. Выбранные интервалы варьирования и уровни факторов указаны в табл. 2.10.
Была реализована полуреплика 24-1 с определяющим контрастом l = х1х2 x3x4.Матрица планирования и результаты опытов представлены в табл. (2.11).
Опыты не дублировали. Для определения дисперсии параметра оптимизации было проведено три опыта при нахождении факторов на основных уровнях (графитовый тигель).
Полученные значения параметра оптимизации 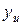 , его среднее значение
, его среднее значение 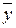 , отклонения значений параметра оптимизации от его среднего значениями
, отклонения значений параметра оптимизации от его среднего значениями 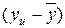 и квадраты этих отклонений приведены в табл. (2.12).
и квадраты этих отклонений приведены в табл. (2.12).
Таблица 2.10
Уровни и интервалы варьирования факторов
| Наименование | Факторы | |||
| х1 | х2 | x3 | x4 | |
| Основной уровень Интервал варьирования Верхний уровень(+) Нижний уровень(–) | 0,40 0,15 0,55 0,25 | – – Графитовый тигель Шамотный тигель |
Таблица 2.11
Матрица планирования
| Номер опыта | Порядок реализации опытов | x0 | x1 | x2 | x3 | x4 | y |
| + | + | + | + | + | |||
| + | – | + | + | – | |||
| + | + | – | + | – | |||
| + | – | – | + | + | |||
| + | + | + | – | – | |||
| + | – | + | – | + | |||
| + | + | – | – | + | |||
| + | – | – | – | – |
Таблица 2.12
Вспомогательная таблица для расчета 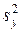
| Номер опыта | 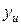
| 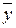
| 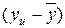
| 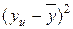
|
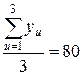
| –2 | |||
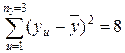
|
 Дисперсия параметра оптимизации:
Дисперсия параметра оптимизации:
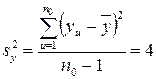 .
.
Находим коэффициенты модели (уравнение регрессии):
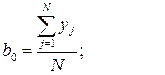
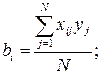
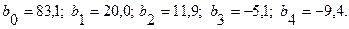
Средняя квадратичная ошибка в определении коэффициентов регрессии
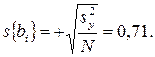
Доверительный интервал коэффициентов регрессии 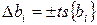 .
.
При 5%–ном уровне значимости и числе степеней свободы 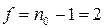 табличное значение критерия
табличное значение критерия 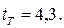 Следовательно,
Следовательно, 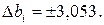 Все коэффициенты регрессии по абсолютной величине больше доверительного интервала, поэтому их можно признать статистически значимыми. Таким образом, получили модель в виде полинома первой степени:
Все коэффициенты регрессии по абсолютной величине больше доверительного интервала, поэтому их можно признать статистически значимыми. Таким образом, получили модель в виде полинома первой степени:
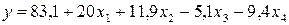 .
.
Согласно полученной модели параметр оптимизации возрастает с увеличением значений факторов х1, х2 и уменьшением значений факторов х3, x4. Наибольшее влияние на параметр оптимизации оказывает фактор х1. Проверку адекватности модели производим по F – критерию Фишера. Для вычисления дисперсии адекватности составим вспомогательную таблицу. 2.13.
Таблица 2.13
Вспомогательная таблица для расчета 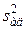
| Номер опыта | 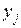
| 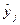
| 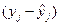
| 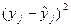
|
| –1 | ||||
| +2 | ||||
| 95. | –1 | |||
| –1 | ||||
| –2 | ||||
| +3 | ||||
| –2 | ||||
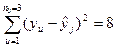
|
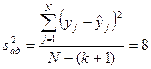 ;
;
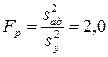 .
.
Табличное значение FT – критерия при 5% – ном уровне значимости и числах степеней свободы для числителя 3 и для знаменателя 2 равно 19,2 FP<FT. Следовательно, модель адекватна. Полученное уравнение используем для крутого восхождения по поверхности отклика. Крутое восхождение (табл 2.14) [3] начинаем из нулевой точки (основные уровни): x1 = 0,40; х2=840; х3=60; х4 – медленное охлаждение (шамотный тигель), так как быстрое охлаждение приводит к уменьшению параметра оптимизации (b4 = – 9,4). Шаг движения для фактора х2 принят 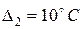 . По формуле (2.31) вычисляем шаг движения для факторов x1 и x3
. По формуле (2.31) вычисляем шаг движения для факторов x1 и x3
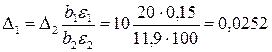
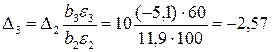 .
.
Таблица 2.14
Расчет крутого восхождения
| Наименование | x1 | х2 | х3 | х4 | y | |
| Основной уровень | 0,40 | – | – | |||
| Коэффициент bi | 11,9 | –5,1 | –9,4 | – | ||
Интервал
варьирования 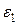
| 0,15 | – | – | |||
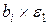
| –306 | – | – | |||
Шаг 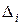
| 0,0252 | –2,57 | – | – | ||
| Округленный шаг | 0,03 | –3 | – | – | ||
| Мысленный опыт | 0,43 | Шамотный тигель | – | |||
| Окончание таблицы 2.14 | ||||||
| То же | 0,46 | То же | – | |||
| Реализованный опыт 9 | 0,49 | – | ||||
| Мысленный опыт | 0,52 | – | – | |||
| То же | 0,55 | – | – | |||
| Реализованный опыт 10 | 0,58 | – | ||||
| Реализованный опыт 11 | 0,61 | – | ||||
| Реализованный опыт 12 | 0,64 | – |
Лучший результат получен в 11-м опыте. Величина параметра оптимизации удовлетворила исследователей, и работа была закончена. Таким образом, потребовалось 12 опытов для того, чтобы определить оптимальные условия модифицирования алюминия молибденом.
Дата добавления: 2019-10-16; просмотров: 1444;
