Исследование области оптимума, представленной полиномом второй степени
В результате выполнения плана второго порядка исследователь получает полином второй степени, адекватно описывающий область оптимума:
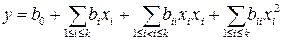 . (3.19)
. (3.19)
Уравнение второй степени в таком виде анализировать сложно, поэтому путем преобразований его приводят к канонической форме. Каноническое преобразование уравнения второй степени заключается в выборе новой системы координат, в которой уравнение принимает более простой вид. Новую систему координат получают путем параллельного переноса старой системы в новое начало и поворота координатных осей относительно этого начала. В результате канонического преобразования уравнение (3.19)приводится к стандартному каноническому уравнению
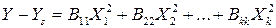 , (3.20)
, (3.20)
где Y – значение параметра оптимизации; Ys– значение параметра оптимизации в новом начале координат; Х1, Х2, ..., Хk – канонические переменные, являющиеся линейными функциями факторов; B1, B2, ..., Bk – коэффициенты уравнения регрессии в канонической форме.
Первым этапом канонического преобразования является перенос начала координат в особую точку – центр поверхности отклика. Для определения координат этой точки исходное уравнение (3.19) дифференцируют по каждой независимой переменной. Приравнивая частные производные нулю, получают систему уравнений
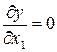 ;
; 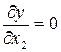 ; …;
; …; 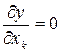 . (3.20)
. (3.20)
При аппроксимации функции отклика полиномом второй степени и дифференцировании его по каждой независимой переменной получают систему k линейных уравнений. Если определитель этой системы уравнений равен нулю, то поверхность отклика не имеет центра. В этом случае начало координат не переносят или переносят в точку с наилучшим значением параметра оптимизации.
Если поверхность имеет центр, т. е. определитель системы отличен от нуля, тогда начало координат переносят в центр. Решая указанную выше систему уравнений, находят координаты центра s поверхности в старой системе координат. При параллельном переносе системы координат в центр s поверхности в исходном уравнении исчезают члены, содержащие линейные эффекты, и изменяется свободный член. Коэффициенты при вторых степенях и взаимодействиях инвариантны относительно переноса. Подставляя найденные значения координат центра s в исходное уравнение, определяют значение параметра оптимизации Ys в центре (в начале новой системы координат).
После параллельного переноса координатных осей исходное уравнение (3.19) принимает вид
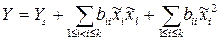 , (3.21)
, (3.21)
где Ys – значение параметра оптимизации в новом начале координат; 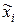 ,
, 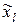 – новые координаты.
– новые координаты.
Вторым этапом канонического преобразования является поворот координатных осей в новом начале координат до совмещения их с главными осями геометрической поверхности, соответствующей изучаемой функции отклика. При повороте координатных осей исчезают члены с эффектами взаимодействия и изменяются коэффициенты при вторых степенях. Свободный член инвариантен относительно поворота координатных осей. В результате поворота осей получают уравнение
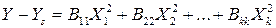 .
.
Для определения коэффициентов B1, B2, ..., Bkk необходимо решить характеристическое уравнение
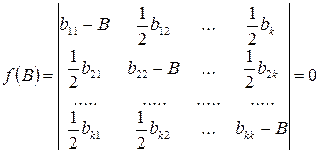 . (3.22)
. (3.22)
Корни этого уравнения и будут искомыми коэффициентами регрессии Вii.
Для пояснения изложенного материала рассмотрим следующий пример. Необходимо привести к канонической форме уравнение, полученное в результате реализации плана второго порядка,
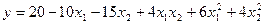 (3.23)
(3.23)
Дифференцируем уравнение по независимым переменным и приравниваем частные производные нулю:
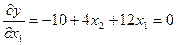 ;
; 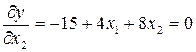 .
.
Вычисляем определитель системы
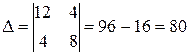 .
.
Определитель не равен нулю, следовательно, исследуемая поверхность имеет центр.
Находим координаты x1s и x2s центра s:
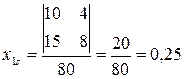 ;
; 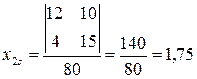 .
.
Подставляя x1s и x2s в уравнение (3.23), находим значение параметра оптимизации Ys в новом начале координат:
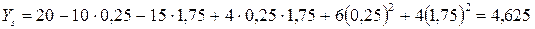 .
.
После параллельного переноса координатных осей уравнение примет вид
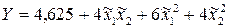 .
.
Для определения коэффициентов B11, B22 решаем следующее характеристическое уравнение:
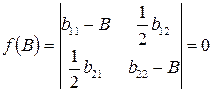 .
.
Подставляя значения b11, b12, b22 получим
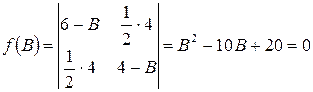 .
.
Решая это квадратное уравнение, находим его корни:
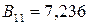 ;
; 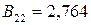 .
.
Правильность вычислений можно проверить сравнением сумм коэффициентов при квадратичных членах в исходном и каноническом уравнениях. При правильно выполненных вычислениях суммы коэффициентов должны быть равны, т. е.
 .
.
Таким образом, уравнение (3.23) в канонической форме имеет вид
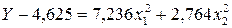 .
.
Уравнение в канонической форме удобно для анализа и оптимизации, так как в него входят все факторы только в квадрате. Величина Y – Ys зависит от знаков коэффициентов Вii и не зависит от направления движения из центра по оси Хi.
Если все коэффициенты Вii отличны от нуля и центр поверхности лежит в области эксперимента, то возможны следующие случаи 1) все коэффициенты Вii<0, тогда движение в любую сторону от центра уменьшает параметр оптимизации; 2) все коэффициенты Вii>0, тогда движение в любую сторону от центра увеличивает параметр оптимизации; 3) часть коэффициентов Вii<0, а часть коэффициентов Вii>0; в этом случае для увеличения параметра оптимизации следует двигаться от центра так, чтобы значения Xi для коэффициентов Вii<0 равнялись нулю, т. е. искать максимум вдоль осей с Вii>0; наоборот, для уменьшения параметра оптимизации следует двигаться только вдоль осей с Вii<0.
При k≤3 после канонического преобразования уравнения регрессии легко определить, к какому типу относится геометрический образ изучаемой функции отклика.
При k = 2 геометрический образ изучаемой функции можно представить в виде контурных линий (изолиний). Возможны четыре типа контурных линий (рис.3.3). Каждая линия представляет собой проекцию сечения поверхности отклика плоскостью, параллельной плоскости чертежа при значениях параметра оптимизации, равных Y1, Y2, Y3, Y4. Такие линии называют линиями равного отклика, так как каждая линия соответствует определенному значению параметра оптимизации.
Эллипсы (рис.3.3 а) соответствуют поверхности отклика, имеющей экстремум в центре s. Коэффициенты В11 и В22 имеют одинаковые знаки. Если коэффициенты отрицательны, то центр фигуры является максимумом, если коэффициенты положительны – минимумом.
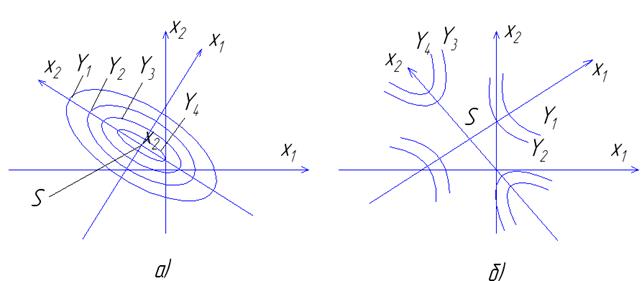
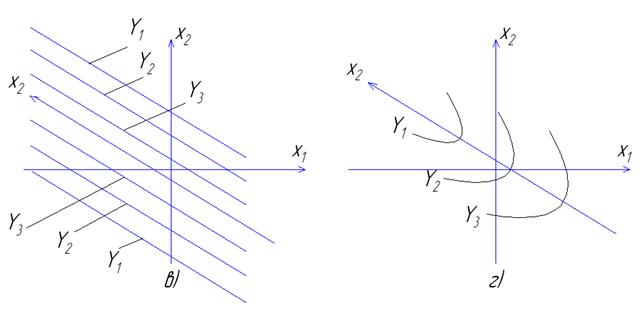 Рис. 3.3 Контурные кривые, характеризующие область оптимума, описываемую уравнением второго порядка при k = 2.
Рис. 3.3 Контурные кривые, характеризующие область оптимума, описываемую уравнением второго порядка при k = 2.
Эллипс вытянут по той оси, которой соответствует меньший по абсолютной величине коэффициент в каноническом уравнении.
Гиперболы (рис.3.3 б) соответствуют поверхности отклика типа минимакса. Коэффициенты В11 и В22 имеют разные знаки.
Параметр оптимизации увеличивается при движении из центра фигуры по одной оси и уменьшается при движении по другой оси. Исследователь выбирает направление движения в зависимости от того, что его интересует – максимум или минимум. Здесь, как и при крутом восхождении, намечается серия мысленных опытов, часть из которых реализуется.
Параллельные линии (рис.3.3 в) соответствуют поверхности отклика, представляющей собой стационарное возвышение. Коэффициент В22 равен нулю. Под определение центра в этом случае подходит любая точка на оси Х2.
Параболы (рис.3.3 г) соответствуют поверхности отклика типа возрастающего возвышения. При коэффициенте В22, равном нулю, центр фигуры находится в бесконечности. Начало координат помещают в точку С вблизи центра эксперимента на оси Х2 и получают уравнение параболы
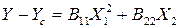 ,
,
где В2 – коэффициент, определяющий крутизну возвышения, т. е. скорость увеличения параметра оптимизации по оси Х2.
Аналогично можно анализировать поверхности отклика, описываемые уравнениями второго порядка, при числе факторов k = 3. Рассмотрим некоторые контурные поверхности, характеризующие область оптимума. Область оптимума характеризуется эллипсоидом вращения (рис.3.4 а) и имеет экстремум в центре эллипсоида, если все коэффициенты Вii канонического уравнения имеют одинаковые знаки. Если два коэффициента имеют одинаковые знаки, а третий близок к нулю, то область оптимума может характеризоваться эллиптическим цилиндром (рис.3.4 б). В этом случае ось цилиндра, соответствующая незначимому коэффициенту, является линией максимума. При близости к нулю одного коэффициента канонического уравнения область оптимума может также характеризоваться эллиптическим параболоидом (рис.3.4 д), при этом центр фигуры находится в бесконечности. Если знак одного из коэффициентов канонического уравнения противоположен знакам двух других, то область оптимума характеризуется одно- или двуполостным гиперболоидом (рис.3.4 г, в). В случае, когда два коэффициента канонического уравнения близки к нулю, область оптимума может характеризоваться серией параллельных плоскостей (рис.3.4 е), одна из которых соответствует наибольшей величине параметра оптимизации.
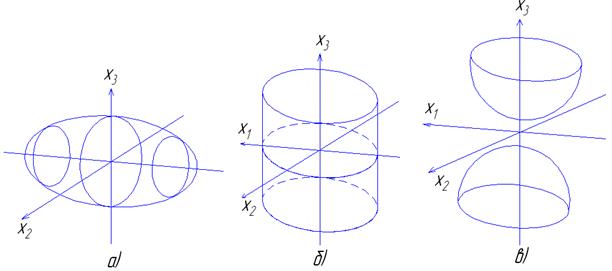
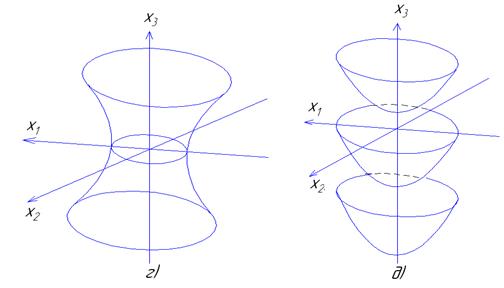
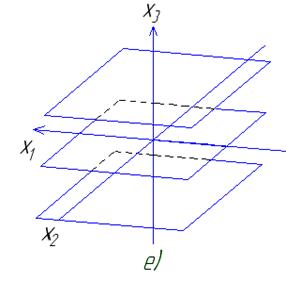
Рис. 3.4. Некоторые трехмерные контурные поверхности, характеризующие область оптимума, описываемую уравнением второго порядка при числе факторов k = 3:
а – эллипсоид вращения; б – эллиптический цилиндр; в – двуполостный гиперболоид; г – однополостный гиперболоид; д – эллиптический параболоид; е –параллельные плоскости одна, из которых соответствует наибольшей величине параметра оптимизации.
При k > 3 наглядное представление о геометрическом образе функции отклика становится невозможным из-за отсутствия у человека геометрической интуиции в многомерных пространствах.
Все многообразие поверхностей отклика, описываемых уравнениями второго порядка, можно проиллюстрировать поверхностями трех следующих типов: 1) поверхности, имеющие экстремум-максимум или минимум (см. рис. 3.3а, 3.4а); в этом случае все коэффициенты канонического уравнения имеют одинаковые знаки; центр фигуры находится вблизи центра эксперимента; 2) поверхности типа минимакса (см. рис.3.3 б; рис.3.4 г); коэффициенты канонического уравнения имеют разные знаки; центр фигуры находится вблизи центра эксперимента; 3) поверхности типа возрастающего возвышения, или гребня (см. рис.3.3 в, г; рис.3.4 д, е); некоторые коэффициенты канонического уравнения близки к нулю; центр фигуры удален от центра эксперимента.
Если поверхность отклика иллюстрируется поверхностями первого типа, то решение экстремальной задачи заканчивают после приведения уравнения к канонической форме. Исследователю остается только провести несколько опытов в центре фигуры и убедиться в том, что экспериментальные данные хорошо совпадают со значениями, предсказанными уравнением регрессии. Ситуация значительно сложнее, если поверхность принадлежит второму или третьему типу. В этих случаях приходится искать условный экстремум в той части факторного пространства, где проводились эксперименты, либо искать его при некоторой разумной экстраполяции. Если поверхность является минимаксом, то в поисках условного максимума двигаются из центра фигуры в прямом или обратном направлениях координатных осей, для которых канонические коэффициенты положительны. В случае нелинейного возрастающего возвышения условный экстремум при ограничениях, наложенных сферой радиуса 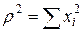 можно искать, пользуясь методом неопределенных множителей Лагранжа. Можно также находить условный экстремум перебором всех комбинаций независимых переменных, варьируя их определенным образом. Решить эту задачу можно только с помощью ЭВМ, так как при каждой комбинации значений независимых переменных необходимо вычислять значение параметра оптимизации.
можно искать, пользуясь методом неопределенных множителей Лагранжа. Можно также находить условный экстремум перебором всех комбинаций независимых переменных, варьируя их определенным образом. Решить эту задачу можно только с помощью ЭВМ, так как при каждой комбинации значений независимых переменных необходимо вычислять значение параметра оптимизации.
Поиск оптимальных условий исследуемого процесса при небольшом числе k влияющих факторов можно упростить, анализируя поверхность отклика в области оптимума графоаналитическим методом с помощью двумерных сечений. Исходное уравнение регрессии в этом случае сводят к уравнению с двумя факторами, стабилизируя остальные на постоянных уровнях. Этим способом можно получить представление о влиянии каждой пары факторов на параметр оптимизаций.
Применение плана второго порядка для исследования аэродинамических потоков, генерируемых дискретными шлифовальными кругами
Дискретные шлифовальные круги с режущей поверхностью, составленной из отдельных абразивных сегментов, генерируют по сравнению со сплошными кругами более мощные аэродинамические потоки, которые могут значительно ухудшать качество обработанных деталей и свести к минимуму достоинства кругов этого класса.
Исследование закономерностей формирования аэродинамических потоков, генерируемых дискретными шлифовальными кругами, позволит разработать научно-обоснованные рекомендации по назначению геометрических параметров дискретных кругов и устройств для подачи смазочно-охлаждающей жидкости (СОЖ), обеспечивающих оптимальные условия для проявления ее функциональных свойств в наибольшей степени.
Для измерения скоростного напора, создаваемого воздушным потоком вращающегося дискретного шлифовального круга, использовали стандартный микроманометр ММН I (рис 3.5), который с помощью резиновой трубки 2 присоединяли к трубке Пито 3, устанавливаемой с помощью держателя в непосредственной близости к вращающемуся сборному дискретному кругу 4 навстречу генерируемому потоку.

Рис. 3.5 Схема измерения скоростного напора, генерируемого сборным шлифовальным кругом:
1 – микроманометр;
2 – резиновая трубка;
3 – трубка Пито;
4 – сборный прерывистый шлифовальный крут.
Для выявления закономерностей формирования аэродинамических потоков вокруг вращающегося прерывистого круга измерения производили при различных положениях трубки Пито по образующей круга (параметр 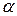 ) и на разных расстояниях от периферии круга (параметр R). Была реализована матрица центрального композиционного планирования второго порядка (табл. 3.11).
) и на разных расстояниях от периферии круга (параметр R). Была реализована матрица центрального композиционного планирования второго порядка (табл. 3.11).
Таблица 3.11
Матрица центрального композиционного планирования 2-го порядка
| № опыта | x0 | 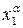
| 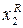
| 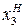
| 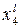
| x1x2 | x1x3 | x1x4 | x2x3 | x2x4 | x3x4 | 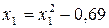
| 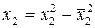
| 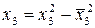
| 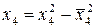
| Примечание |
| в0 | в1 | в2 | в3 | в4 | в12 | в13 | в14 | в23 | в24 | в34 | в11 | в22 | в33 | в44 | ||
| ++ | + | + | + | + | + | + | + | + | + | + | 0,31 | 0,31 | 0,31 | 0,31 | Полный факторный эксперимент 24=16 | |
| ++ | – | + | + | + | – | – | – | + | + | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++1 | + | – | + | + | – | + | + | – | – | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | – | + | + | + | – | – | – | – | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | + | + | – | + | + | – | + | – | + | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | + | – | + | – | + | – | – | + | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | + | – | – | + | – | – | + | + | – | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | – | – | + | + | + | – | + | – | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | + | + | + | – | + | + | + | + | – | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | + | + | – | – | – | – | + | – | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| Продолжение таблицы 3.11 | ||||||||||||||||
| + | – | + | – | – | + | + | – | + | – | 0,31 | 0,31 | 0,31 | 0,31 | |||
| ++ | – | – | + | – | + | – | – | – | + | – | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | + | + | – | – | + | – | + | – | – | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | + | – | – | – | + | – | – | – | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | + | – | – | – | – | – | + | + | + | + | 0,31 | 0,31 | 0,31 | 0,31 | ||
| ++ | – | – | – | – | + | + | – | + | + | + | 0,31 | 0,31 | 0,31 | 0,31 |
| Окончание таблицы 3.11 | ||||||||||||||||
| + | +1,414 | 1,31 | –0,69 | –0,69 | –0,69 | Звездные точки | ||||||||||
| ++ | –1,414 | 1,31 | –0,690 | –0,69 | –0,69 | |||||||||||
| ++ | +1,414 | –0,69 | 1,31 | –0,69 | –0,69 | |||||||||||
| ++ | –1,414 | –0,69 | 1,31 | –0,69 | –0,69 | |||||||||||
| ++ | +1,414 | –0,69 | –0,69 | 1,31 | –0,69 | |||||||||||
| ++ | –1,414 | –0,69 | –0,69 | 1,31 | –0,69 | |||||||||||
| ++ | +1,414 | –0,69 | –0,69 | –0,69 | 1,31 | |||||||||||
| ++ | –1,414 | –0,69 | –0,69 | –0,69 | 1,31 | |||||||||||
| ++ | –0,69 | –0,69 | –0,69 | –0,69 | Нулевая точка | |||||||||||
| ++ | –0,69 | –0,69 | –0,69 | –0,69 | ||||||||||||
| +++ | –0,69 | –0,69 | –0,69 | –0,69 | ||||||||||||
| +++ | –0,69 | –0,69 | –0,69 | –0,69 | ||||||||||||
| + | –0,69 | –0,69 | –0,69 | –0,69 |
В результате проведенных предварительных экспериментов, определены факторы и границы их варьирования. В качестве варьируемы факторов выбраны: расстояние от левого торца абразивных сегментов до трубки Пито, дискретно перемещаемой вдоль образующей инструмента 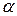 (X1) , расстояние от трубки Пито до периферийной режущей поверхности круга R (Х2), высота сегментов H (Х3) и расстояние между соседними сегментами l (Х4) (см. pиc 3.5). Значения уровней перечисленных переменных факторов представлены в табл. 3.12.
(X1) , расстояние от трубки Пито до периферийной режущей поверхности круга R (Х2), высота сегментов H (Х3) и расстояние между соседними сегментами l (Х4) (см. pиc 3.5). Значения уровней перечисленных переменных факторов представлены в табл. 3.12.
Таблица 3.12
Численные значения уровней переменных
| Факторы | 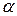 , мм , мм
| Rмм | Н, мм | l, мм |
| 1.Код | X1 | X2 | X3 | X4 |
| 2.Основной уровень | 7,5 | 6,25 | 12,5 | |
| 3. Интервалы варьирования | 4,6 | 2,65 | 5,3 | |
| 4.Верхний уровень (+1) | 12,1 | 8,9 | 17,8 | |
| 5.Нижний уровень (–1) | 2,9 | 3,6 | 7,2 | |
6.Звездная точка ( 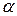 = +1,414) = +1,414)
| ||||
7.Звездная точка ( 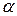 = –1,414) = –1,414)
| 2,5 | |||
| 8.Нулевая точка | 7,5 | 6,25 | 12,5 |
Зависимости, связывающие скорость воздушных потоков, генерируемых сборным абразивным кругом, с указанными факторами отыскивали в виде
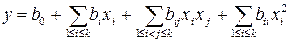 , (3.24)
, (3.24)
где y – исследуемый параметр, т.е. скорость воздушного потока в кодовом обозначении, k – число факторов, 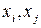 – кодовое обозначение переменных факторов, во, вi, вj, вij – коэффициенты уравнения регрессии.
– кодовое обозначение переменных факторов, во, вi, вj, вij – коэффициенты уравнения регрессии.
Обработка результатов эксперимента методом математической статистики позволила получить уравнение регрессии, связывающее скорость воздушного потока с конструктивными элементами сборного абразивного круга и координатами точек расположения трубки Пито относительно круга. После проверки значимости коэффициентов регрессии (при уровне значимости 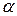 =0,05), проверки с помощью критерия Фишера модели на адекватность и перехода к натуральным значениям факторов по формулам
=0,05), проверки с помощью критерия Фишера модели на адекватность и перехода к натуральным значениям факторов по формулам
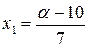 ,
, 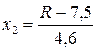 ,
, 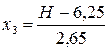 ,
, 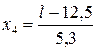
получили
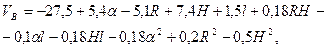 (3.25)
(3.25)
где VB – скорость воздушного потока, генерируемого сборным абразивным кругом в процессе работы.
Анализ уравнения (3.25) показывает, что наибольшее влияние на скорость воздушного потока оказывают расстояния, на которые отстоит трубка Пито от левого торца абразивных сегментов (фактора 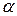 ) и от периферийной режущей поверхности (фактора R).
) и от периферийной режущей поверхности (фактора R).
Зависимости 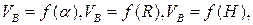 описываются полными трехчленами, содержащими фактор во второй, первой и нулевой степени и представляющими собой параболы с различным расположением вершины и ветвей. Парабола
описываются полными трехчленами, содержащими фактор во второй, первой и нулевой степени и представляющими собой параболы с различным расположением вершины и ветвей. Парабола 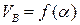 имеет вершину, лежащую на прямой, параллельной оси y и отстоящей от начала координат по оси x на расстоянии, примерно равном половине длины образующей абразивных сегментов.
имеет вершину, лежащую на прямой, параллельной оси y и отстоящей от начала координат по оси x на расстоянии, примерно равном половине длины образующей абразивных сегментов.
Ветви параболы 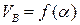 направлены вниз (рис.3.6.) В области, прилегающей к торцам инструмента, скорость воздушных потоков в радиальном направлении принимает весьма малые численные значения, в то время как в поперечной плоскости симметрии абразивных сегментов скорость воздуха достигает максимальных значений.
направлены вниз (рис.3.6.) В области, прилегающей к торцам инструмента, скорость воздушных потоков в радиальном направлении принимает весьма малые численные значения, в то время как в поперечной плоскости симметрии абразивных сегментов скорость воздуха достигает максимальных значений.
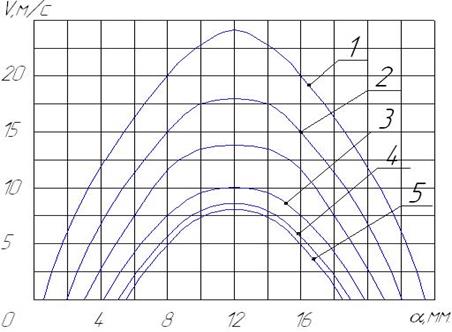
Рис. 3.6 Изменение скорости аэродинамических потоков вдоль образующей режущей поверхности сборного прерывистого абразивного круга.
1. 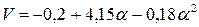 при
при 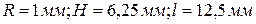
2. 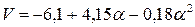 при
при 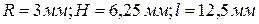
3. 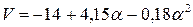 при
при 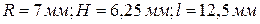
4. 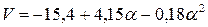 при
при 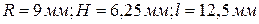
5. 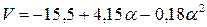 при
при 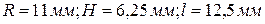
С увеличением расстояния R трубки Пито от рабочей поверхности инструмента скорость воздушного потока быстро уменьшается (рис.3.7), что объясняется торможением воздушного потока окружающим, вовлекаемым в движение воздухом, находившимся ранее в покое. Высота Н абразивных сегментов оказывает значительно меньшее влияние на скорость воздушного потока, чем факторы 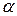 и R. В зависимости от численных значений, входящих в формулу (3.25) факторов, кривая
и R. В зависимости от численных значений, входящих в формулу (3.25) факторов, кривая 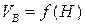 располагается на различном расстоянии от оси абсцисс, максимальное значение скорости достигается при Н 4,5...5,5 мм.
располагается на различном расстоянии от оси абсцисс, максимальное значение скорости достигается при Н 4,5...5,5 мм.
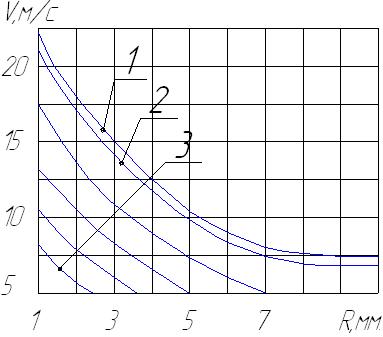
Рис. 3.7 Скорость воздушного потока, генерируемого сборным прерывистым абразивным кругом, в функции радиального расстояния.
1. 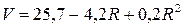 при
при 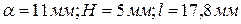
2. 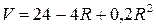 при
при 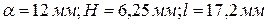
3. 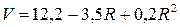 при
при 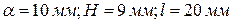 .
.
Расстояние между абразивными сегментами по сравнению с факторами 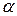 , R, и Н влияет на скорость воздушного потока в самой незначительной степени. Функция
, R, и Н влияет на скорость воздушного потока в самой незначительной степени. Функция 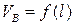 подчиняется линейному закону.
подчиняется линейному закону.
Таким образом, максимальные значения скоростей воздушных потоков, генерируемых сборным абразивным кругом, наблюдаются в области, расположенной в непосредственной близости к режущей поверхности круга и поперечной плоскости симметрии высоты абразивного слоя.
Это обстоятельство свидетельствует о том, что подача СОЖ струей (даже под давлением), направленной радиально к центру круга, не позволит обеспечить эффективное действие СОЖ, поскольку проникновению СОЖ в зону резания будет препятствовать мощный скоростной воздушный напор.
Измерения статического давления воздуха внутри корпуса сборного прерывистого круга, показали, что в этой области создается за счет вращения инструмента разрежение, которое способствует проникновению направленной струи СОЖ внутрь инструмента.
Этот факт положительно сказывается на эффективном охлаждении обрабатываемой поверхности, поскольку СОЖ, всасываясь внутрь круга и вовлекаясь во вращение, мгновенно выбрасывается центробежной силой из инструмента непосредственно в зону резания.
Выполненные исследования аэродинамических потоков позволили найти область, из которой целесообразна подача СОЖ в зону резания, а также найти конструктивное оформление устройства для подачи СОЖ при шлифовании сборными прерывистыми кругами.
Результаты проведенных планируемых многофакторных экспериментов при исследовании аэродинамических потоков, генерируемых прерывистым абразивным кругом, позволили научно обосновать способ подачи СОЖ, обеспечивший значительное улучшение всех параметров качества деталей, повышение производительности процесса обработки и периода стойкости инструмента.
Применение планирования экспериментов при механической обработке материалов
Исследование шероховатости поверхности с использованием ротатабельного планирования
Изготовление прецизионных деталей из пластмасс часто производится обработкой резанием. Выбор рациональных режимов резания в значительной степени определяет производительность процесса и качество обработанной поверхности. В работе [3] предусматривалось установление влияния режимов резания на шероховатость поверхности при точении капролона марки С и поиск условий, обеспечивающих минимальную шероховатость обработанной поверхности. Исследования проводились на высокоскоростном токарном станке. В качестве режущего инструмента использовались резцы с пластинками из твердого сплава ВК6М со следующими геометрическими параметрами: передний угол 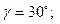 задний угол
задний угол 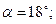 угол наклона главной режущей кромки
угол наклона главной режущей кромки 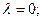 радиус закругления при вершине резца
радиус закругления при вершине резца 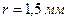 . Шероховатость поверхности режущего инструмента соответствовала
. Шероховатость поверхности режущего инструмента соответствовала 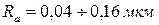 . Обработке подвергались блоки из капролона без охлаждения.
. Обработке подвергались блоки из капролона без охлаждения.
За критерий оценки шероховатости принимали высоту неровностей Rz, которая определялась по десяти измерениям каждого участка. В качестве факторов выбраны скорость резания v, подача s и глубина резания t, т.к. эти элементы режима в основном и определяют высоту неровностей обработанной поверхности. В качестве параметра оптимизации принимаем высоту неровностей.
На первом этапе исследования был поставлен полный факторный эксперимент типа 23. Уровни факторов и интервалы варьирования выбраны по результатам предварительных поисковых экспериментов. Уровни и интервалы варьирования факторов приведены в табл. (4.1). Матрица плана эксперимента и результаты измерений высоты неровностей у представлены в табл. (4.2).
Таблица 4.1
Уровень и интервалы планирования факторов
| Факторы | Уровни | Интервалы варьирования | ||
| верхний +1 | основной 0 | нижний –1 | ||
| x1 – скорость резания, м/мин x2 – подача, мм/об x3 – глубина резания, мм | 0,7 0,75 | 0,5 0,5 | 0,3 0,25 | 0,2 0,25 |
Таблица 4.2
План эксперимента типа 23
| Номер опыта | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2 x3 | x1x2x3 | y(Rz) |
| + | – | – | – | + | + | + | – | 2,16 | |
| + | + | – | – | – | – | + | + | 2,65 | |
| + | – | + | – | – | + | – | + | 3,80 | |
| + | + | + | – | + | – | – | – | 4,70 | |
| + | – | – | + | + | – | – | + | 2,22 | |
| + | + | – | + | – | + | – | – | 2,48 | |
| + | – | + | + | – | – | + | – | 4,20 | |
| + | + | + | + | + | + | + | + | 4,89 |
План типа 23 позволяет получить раздельные оценки для коэффициентов уравнения регрессии вида
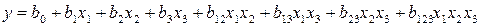 . (4.1)
. (4.1)
Коэффициенты уравнения регрессии (4.1) определяли по формулам
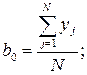
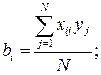
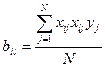 .
.
В результате расчетов были получены следующие значения коэффициентов: b0 = 3,3875; b1 = 0,2925; b2=1,01; b3 = 0,06; b12=0,105; b13= - 0,055; b23 = 0,0875; b123 = 0,0025.
После подстановки значений коэффициентов уравнение (4.1) приняло вид
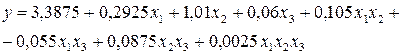 . (4.2)
. (4.2)
Для проверки адекватности полученного уравнения и определения дисперсий коэффициентов необходимо знать дисперсию 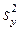 воспроизводимости эксперимента. Находим ее по результатам шести опытов, поставленных в центре плана (опыты 1–6, табл.4.3).
воспроизводимости эксперимента. Находим ее по результатам шести опытов, поставленных в центре плана (опыты 1–6, табл.4.3).
Таблица 4.3
Результаты опытов в центре плана и в «звездных» точках
| Содержание плана | Номер опыта | х0 | x1 | x2 | x3 | 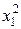
| 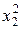
| 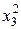
| y |
| Опыты в центре плана | + | 2,31 | |||||||
| + | 2,08 | ||||||||
| + | 2,12 | ||||||||
| + | 2,32 | ||||||||
| + | 2,36 | ||||||||
| + | 2.12 | ||||||||
| Опыты в «звездных» точках | + | –1,682 | 2,828 | 3,55 | |||||
| + | +1,682 | 2,828 | 4,50 | ||||||
| + | –1,682 | 2,828 | 1,80 | ||||||
| + | +1,682 | 2,828 | 5,15 | ||||||
| + | –1,682 | 2,828 | 2,32 | ||||||
| + | +1,682 | 2,828 | 2,56 |
Среднее арифметическое значение параметра оптимизации 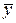 в центре плана
в центре плана
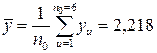 .
.
Дисперсия 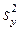 воспроизводимости эксперимента
воспроизводимости эксперимента
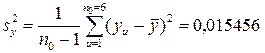 .
.
Разность между значением параметра оптимизации 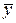 в центре плана и величиной свободного члена b0
в центре плана и величиной свободного члена b0
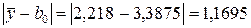 .
.
Полученная разность во много раз превышает ошибку 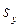 эксперимента:
эксперимента:
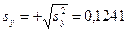 .
.
Из этого следует, что коэффициенты при квадратичных членах значимо отличаются от нуля, а исследуемая зависимость не может быть с достаточной точностью аппроксимирована уравнением (4.1). Поэтому перешли к планированию второго порядка и аппроксимировали неизвестную функцию отклика полиномом вида
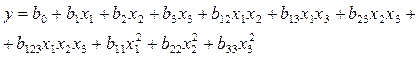 (4.3)
(4.3)
Эксперимент был поставлен по программе центрального композиционного ротатабельного планирования второго порядка Реализованные восемь опытов полного факторного эксперимента 23 (cм. табл. 4.1) и шесть опытов в центре плана (см. табл. 4.2) дополнили шестью опытами в «звездных» точках (опыты 7–12, табл. 4.3). Beличина «звездного» плеча 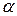 в рассматриваемом случае равна 1,682.
в рассматриваемом случае равна 1,682.
Получили следующие значения коэффициентов регрессии:
b0 = 2, 1956; b1 = 0, 2882; b2 = 0, 9819; b3 = 0, 0646; b12 = 0,105; b13 = 0,055; b23 = 0, 0875; b123 = 0, 0025; b11 = 0, 6663; b22 = 0, 4594; b33 = 0, 0833.
После подстановки значений коэффициентов в уравнение (4.3) оно получим вид
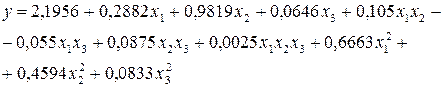 (4.4)
(4.4)
Вычисленные дисперсии коэффициентов регрессии, имеют следующие значения:
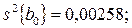
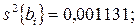
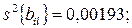
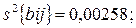
Доверительные интервалы для коэффициентов равны:
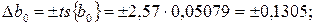
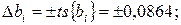
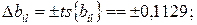
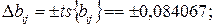
В связи с тем, что коэффициенты b3, b12, b13, b23, b123, b33 по абсолютной величине меньше соответствующих доверительных интервалов, то их можно признать статистически незначимыми и исключить из уравнения регрессии. Так как среди незначимых оказался и коэффициент b33 при квадратичном члене, значимые коэффициенты были пересчитаны с использованием метода наименьших квадратов. Пересчитанные значения коэффициентов оказались следующими: b0 = 2,26; b11 = 0,6555; b22 = 0,4389; b1 = 0,2882; b2 = 0,9819.
Таким образом, математическая модель, полученная в результате ротатабельного планирования второго порядка, приняла вид
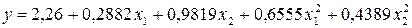 . (4.5)
. (4.5)
Для проверки адекватности модели (4.5) вычислили дисперсию 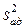 адекватности по формуле
адекватности по формуле
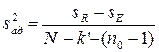 .
.
Остаточная сумма квадратов
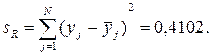
Найденная сумма квадратов sE и использованная для определения дисперсии параметра оптимизации, равна 0,077284. При указанных значениях sR и sE дисперсия 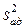 = 0,0333. Определяем расчетное значение F – критерия:
= 0,0333. Определяем расчетное значение F – критерия:
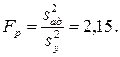
При 5%-ном уровне значимости и числах степеней свободы для числителя 10 и знаменателя 5 табличное значение критерия Fт равно 4,74. Значение FP<FT поэтому модель (4.5) следует признать адекватной. Уравнение (4.5) неудобно для интерпретации полученных результатов и практических расчетов, поэтому его преобразовали по формулам перехода от кодированных значений (х1, х2, х3) к натуральным значениям факторов (v, s, t):
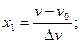
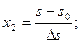
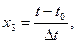
где v0, s0, t0 – натуральные значений факторов на основных уровнях; 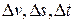 – значения интервалов варьирования.
– значения интервалов варьирования.
Таким образом, 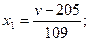
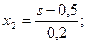
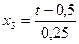 . (4.6)
. (4.6)
Уравнение (4.5) с учетом выражений (4.6) примет вид:
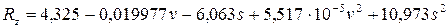 . (4.7)
. (4.7)
Из приведенного выражения следует, что в области эксперимента 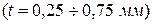 глубина резания не оказывает влияния на шероховатость обработанной поверхности капролона.
глубина резания не оказывает влияния на шероховатость обработанной поверхности капролона.
Уравнение (4.5) используем для поиска оптимального режима обработки капролона резцом с заданной геометрией. В результате переноса начала координат в центр фигуры с координатами x1s = –0,22; х2s = –1,12 (они соответствуют значениям v=181м/мин; s = 0,276 мм/об) и поворота координатных осей уравнение (4.5) было приведено к каноническому виду
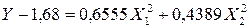 (4.8)
(4.8)
Выражение (4.8) является уравнением эллипса в каноническом виде. Так как коэффициенты b11 и b22 имеют положительные знаки, центр эллипсов (x1s = –0,22; х2s = –1,12) является минимумом функции отклика. В этом случае для поиска экстремума достаточно поставить опыт в центре фигуры и проверить, насколько точно значение параметра оптимизации, предсказанное уравнением регрессии, совпадает с экспериментальным.
В дополнительном опыте, поставленном в центре фигуры (x1s = –0,22; х2s = –1,12), получено значение функции отклика у = 1,7 мкм. Дальнейшее варьирование скорости и подачи вблизи экстремума не вызвало уменьшения значения у. Таким образом, оптимальным следует считать режим: v=181 м/мин, s = 0,276 мм/об при 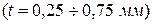 .
.
Уравнение (4.8) можно также использовать для определения ожидаемой шероховатости поверхности при обработке капролона на режимах, входящих в область эксперимента.
Процессы обработки материалов резанием являются сложными многофакторными процессами. В этих процессах исследуемая величина часто является случайной величиной, зависящей от большого числа контролируемых и неконтролируемых факторов. Поэтому процессы резания все чаще стали рассматривать с вероятностно-статистических позиций, а при экспериментальных исследованиях применять методы планирования эксперимента, базирующиеся на идеях математической статистики.
Дата добавления: 2019-10-16; просмотров: 1561;
