Оптимизация геометрии режущего инструмента на основе метода крутого восхождения по поверхности отклика.
При поиске оптимальных условий протекания различных процессов обработки материалов резанием может быть с успехом использован метод крутого восхождения. Этот метод позволяет резко сократить число опытов, получить количественные оценки влияния отдельных факторов и их взаимодействий на изучаемый параметр, установить оптимальные значения параметров процесса или оптимальные значения параметров инструмента. Так, например, требуется установить влияние заднего угла 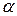 , переднего угла
, переднего угла 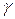 , главного угла в плане
, главного угла в плане 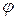 , вспомогательного угла в плане
, вспомогательного угла в плане 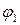 , радиуса при вершине r на стойкость Т токарного резца и определить значения этих геометрических параметров, обеспечивающие, максимальную стойкость резца при обработке аустенитной стали на заданном режиме. На основании априорной информации были выбраны основные уровни и интервалы варьирования факторов (табл. 4.4).
, радиуса при вершине r на стойкость Т токарного резца и определить значения этих геометрических параметров, обеспечивающие, максимальную стойкость резца при обработке аустенитной стали на заданном режиме. На основании априорной информации были выбраны основные уровни и интервалы варьирования факторов (табл. 4.4).
Таблица 4.4
Уровни и интервалы варьирования факторов
| Факторы, град | Кодовое обозначение | Интервалы варьирования | Уровни факторов | ||
| верхний + 1 | основной 0 | нижний –1 | |||
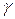 – передний угол – передний угол
| x1 | –3 | –5 | –7 | |
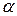 – задний угол – задний угол
| x2 | ||||
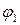 – вспомогательный угол в плане – вспомогательный угол в плане
| x3 | ||||
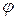 – главный угол в плане – главный угол в плане
| x4 | ||||
| r – радиус при вер- шине, мм | x5 | 0,5 | 1,5 | 1.0 | 0,5 |
Таблица 4.5
Матрица планирования и результаты опытов
| Номер опыта | x0 | x1 | x2 | x3 | x4 | x5 | Y(T), мин |
| + | – | – | – | + | – | 34,7 | |
| + | + | – | – | – | + | 29,8 | |
| + | – | + | – | – | + | 42,5 | |
| + | + | + | – | + | – | 39,2 | |
| + | – | – | + | + | + | 35,5 | |
| + | + | – | + | – | – | 16,7 | |
| + | – | + | + | – | – | 31,0 | |
| + | + | + | + | + | + | 39,6 |
Приняв в качестве параметра оптимизации период стойкости Т резца и обозначив его через у, использовали для крутого восхождения линейную модель
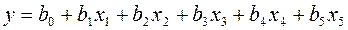 .
.
На первом этапе исследования в качестве плана эксперимента приняли 1/4-реплику (25-2) от полного факторного эксперимента 25.Реплика задана генерирующими соотношениями x4=x1x2; x5=x1x2x3.Матрица планирования и результаты опытов приведены в табл. 4.5.
Значения коэффициентов находили по формуле
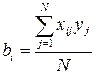 ,
,
где
xij – кодированное значение (±1)
i-гo фактора в j-м опыте;
yi – значение параметра оптимизации в j -м опыте;
N – число опытов в матрице планирования.
Например:
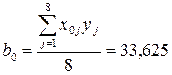 ;
;
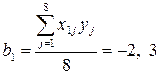 и т.д.
и т.д.
Для остальных коэффициентов получили следующие значения: b2=4,45; b3 = –2,925; b4 = 3,625; b5=3,225.
Дисперсию 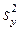 параметра оптимизации вычисляли по результатам четырех опытов в центре плана, т. е. при x1=x2=x3=x4=x5=0.
параметра оптимизации вычисляли по результатам четырех опытов в центре плана, т. е. при x1=x2=x3=x4=x5=0.
Расчет дисперсии 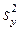 приведен в табл. (4.6).
приведен в табл. (4.6).
Дисперсии коэффициентов регрессии
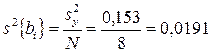 .
.
Доверительный интервал коэффициентов
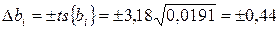 .
.
где,
t – табличное значение критерия Стьюдента, равное 3,18 при 5%-ном уровне значимости и числе степеней свободы f=3.
Примечание. n0 – число опытов в центре плана;
yu – значение параметра оптимизации в u-м опыте в центре плана.
Так как абсолютные величины коэффициентов регрессии больше доверительного интервала, то все они являются статистически значимыми.
Уравнение регрессии с кодированными переменными имеет вид
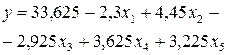 . (4.8)
. (4.8)
Таблица 4.6
Вспомогательная таблица расчета 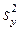
| Номер опыта в центре плана | yu | 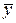
| 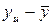
| 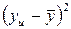
| 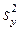
|
| 33,1 | 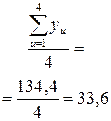
| –0,5 | 0,25 | 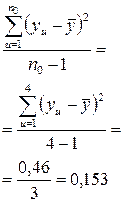
| |
| 33,5 | –0,1 | 0,01 | |||
| 34,0 | 0,4 | 0,15 | |||
| 33,8 | 0,2 | 0,04 | |||
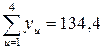
| 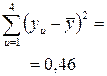
|
Примечание. n0 – число опытов в центре плана; yu – значение параметра оптимизации в u-м опыте в центре плана. Так как абсолютные величины коэффициентов регрессии больше доверительного интервала, то все они являются статистически значимыми.
Уравнение регрессии с кодированными переменными имеет вид
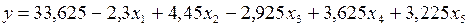 . (4.9)
. (4.9)
Для проверки гипотезы адекватности модели, представленной уравнением (4.9) находим дисперсию адекватности
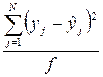 (4.10)
(4.10)
где,
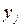 – экспериментальное значение параметра оптимизации в j-м опыте;
– экспериментальное значение параметра оптимизации в j-м опыте; 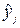 – значение параметра оптимизации в j-м опыте, вычисленное по уравнению (4.9);
– значение параметра оптимизации в j-м опыте, вычисленное по уравнению (4.9);
f – число степеней свободы, f=N–(k+1)
k – число факторов, равное 5.
Для вычисления суммы, входящей в выражение (4.10), составляем вспомогательную таблицу (табл.4.7). При вычислении значений 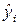 в уравнение (4.9) необходимо подставлять кодированные значения факторов. Например, в первом опыте кодированные значения факторов
в уравнение (4.9) необходимо подставлять кодированные значения факторов. Например, в первом опыте кодированные значения факторов 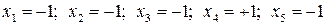 .Следовательно,
.Следовательно, 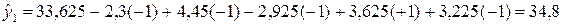 .
.
Подставляя полученное значение суммы (см. табл. 4.7) в выражение (4.2) находим
Таблица 4.7
Вспомогательная таблица расчета 
| Номер опыта | yj | 
| 
| 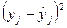
| Номер опыта | yj | 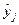
| 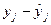
| 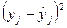
|
| 34,7 | 34,8 | –0,1 | 0,01 | 16,7 | 17,1 | –0,4 | 0,16 | ||
| 29,8 | 29,4 | 0,4 | 0,16 | 31,0 | 30,6 | 0,4 | 0,16 | ||
| 42,5 | 42,9 | –0,4 | 0,16 | 39,6 | 39,7 | –0,1 | 0,01 | ||
| 39,2 | 39,1 | 0,1 | 0,01 | ||||||
| 35,5 | 35,4 | 0,1 | 0,01 | ||||||
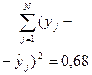
|
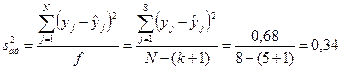 .
.
Дисперсию адекватности можно также определить по выражению
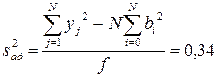 .
.
Дисперсия 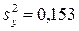 (см. табл. 4.8). Проверку гипотезы адекватности модели производили по F – критерию Фишера. Для этого находили расчетное значение критерия
(см. табл. 4.8). Проверку гипотезы адекватности модели производили по F – критерию Фишера. Для этого находили расчетное значение критерия
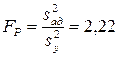 .
.
При 5%-ном уровне значимости и числах степеней свободы для числителя f1=2 и для знаменателя f2=3 табличное значение критерия FT = 9,55. Так как FP<FT, то модель, представленная уравнением (4.9) адекватна.
Убедившись в адекватности уравнения (4.9) переходим к крутому восхождению. Крутое восхождение начинаем из центра плана, т. е. из точки с координатами 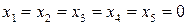 ,что соответствует
,что соответствует 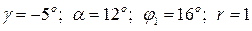 мм. Шаг движения по градиенту для радиуса r принимаем равным Δ5=0,3. Для остальных факторов шаг движения Δi вычисляем по формуле
мм. Шаг движения по градиенту для радиуса r принимаем равным Δ5=0,3. Для остальных факторов шаг движения Δi вычисляем по формуле
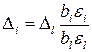 ,
,
где Δl – принятый шаг движения по градиенту для l-го фактора; εi, εl – интервалы варьирования i-гo и l-гофакторов. Например, для первого фактора у шаг движения по градиенту
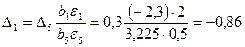 ,
,
или округленно 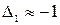 . Шаг движения по градиенту для остальных факторов указан в (табл. 4.8).
. Шаг движения по градиенту для остальных факторов указан в (табл. 4.8).
Таблица 4.8
Расчет крутого восхождения в область оптимума
| Наименование | 
| 
| 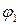
| 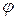
| 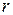
| 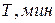
|
| Основной уровень | –5 | 1.0 | – | |||
Коэффициент 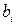
| –2,3 | 4,45 | –2,925 | 3,625 | 3,225 | – |
Интервал варьирования 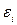
| 0,5 | – | ||||
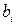 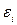
| –4,6 | 8,9 | –11,7 | 36,25 | 1,6125 | – |
| Шаг движения по градиенту | –0,86 | 1,66 | –2,18 | 6,74 | 0,3 | – |
| Округленный шаг | –1 | –2 | 0,3 | – | ||
| Опыт 9 мысленный | –6 | 1,3 | – | |||
| Опыт 10 реализованный | –7 | 1,6 | 45,0 | |||
| Опыт 11 реализованный | –8 | 1,9 | 52,9 | |||
| Опыт 12 реализованный | –9 | 2,2 | 50,3 |
Вычислив шаг движения по градиенту для каждого фактора, приступаем к расчету опытов в направлении градиента. Для расчета условий первого опыта к основному уровню каждого из факторов необходимо прибавить соответствующее значение шага движения по градиенту. Для определения условий каждого последующего опыта к значению каждого из факторов в предыдущем опыте необходимо прибавить соответствующее значение шага. Например, в первом опыте в направлении градиента (опыт 9, табл. 4.8) значения факторов должны быть следующими:
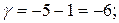
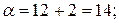
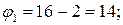
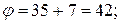
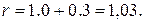
Опыты 10, 11 и 12 реализованы. В опыте 11 получена максимальная стойкость резца T=52,9 мин. После определения условий наилучшего опыта можно закончить исследование, если полученное значение параметра оптимизации устраивает исследователя. Если есть основания считать, что область оптимума не достигнута, то необходимо, приняв условия наилучшего опыта за центр плана, провести новую серию опытов, вычислить коэффициенты линейной модели и вновь произвести крутое восхождение. При решении данной задачи оптимальная геометрия токарного резца 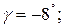
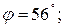
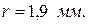
4.3. Применение ротатабельного планирования второго порядка для исследования процесса торцового фрезерования
Требовалось установить зависимость максимальной тангенциальной составляющей РT силы резания от элементов геометрии зуба торцовой фрезы при фрезеровании высокопрочного чугуна. В качестве влияющих факторов рассматривали следующие элементы геометрии зуба фрезы: главный угол 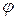 в плане, угол наклона
в плане, угол наклона 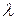 режущей кромки и передний угол
режущей кромки и передний угол 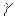 . Зависимость
. Зависимость 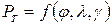 было решено аппроксимировать полиномом второй степени. Эксперимент проведен по программе центрального композиционного ротатабельного планирования второго порядка. Принятые в исследовании уровни и интервалы варьирования факторов указаны в (табл.4.9).
было решено аппроксимировать полиномом второй степени. Эксперимент проведен по программе центрального композиционного ротатабельного планирования второго порядка. Принятые в исследовании уровни и интервалы варьирования факторов указаны в (табл.4.9).
Таблица 4.9
Уровни и интервалы варьирования факторов
| Факторы, град | Код | Интервалы варьирования | Натуральные уровни факторов, соответствующие кодированным | |||||||
| - | - | - | +1,682 | +1 | –1 | –1,682 | ||||
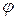 – главный угол в плане – главный угол в плане
| 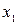
| |||||||||
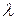 – угол наклона режущей кромки – угол наклона режущей кромки
| 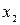
| –1 | –5 | |||||||
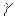 – передний угол – передний угол
| 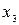
| |||||||||
Матрица планирования и результаты опытов приведены в табл. 4.10. Центральный композиционный ротатабельный план второго порядка для трех факторов состоит из плана полного факторного эксперимента типа 23 (см. табл. 4.10, опыты 1–8), шести опытов в «звездных точках» (опыты 9–14) и шести опытов в центре плана (опыты 15–20).
По результатам опытов, выполненных в соответствии с принятым планом эксперимента, можно оценить коэффициенты уравнения регрессии вида
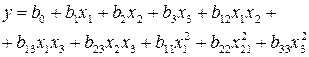 (4.11)
(4.11)
Коэффициенты уравнения (4.11)определяем по формулам
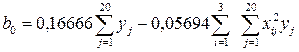
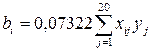 ;
; 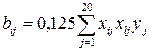 ;
;
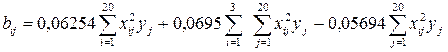 .
.
По данным (табл. 4.10) суммы, входящие в формулы для расчета коэффициентов уравнения:
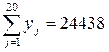 ;
; 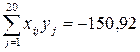 ;
; 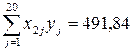 ;
;
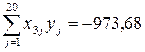 ;
;
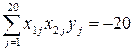 ;
; 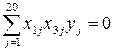 ;
;
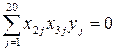 ;
; 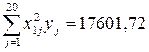 ;
;
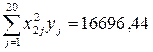 ;
; 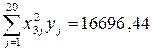 ;
; 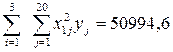 .
.
Используя приведенные выше формулы, находим коэффициенты уравнения регрессии (4.3):
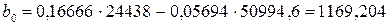 ;
;
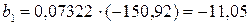 ;
;
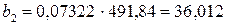 ;
;
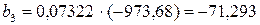 ;
;
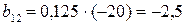 ;
;
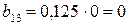 ;
;
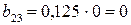 ;
;
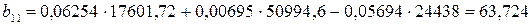 ;
;
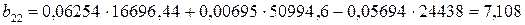 ;
;
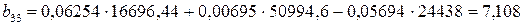 ;
;
Дисперсию 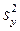 воспроизводимости определяем по результатам опытов в центре плана. Для вычисления
воспроизводимости определяем по результатам опытов в центре плана. Для вычисления 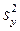 составили вспомогательную таблицу (табл. 4.11) Дисперсии, характеризующие ошибки в определении коэффициентов уравнения регрессии, вычисляли по формулам при k=3 эти формулы примут вид
составили вспомогательную таблицу (табл. 4.11) Дисперсии, характеризующие ошибки в определении коэффициентов уравнения регрессии, вычисляли по формулам при k=3 эти формулы примут вид
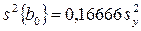 ;
; 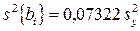 ;
;
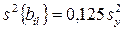 ;
; 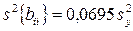 .
.
Дисперсии коэффициентов уравнения регрессии
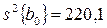 ;
; 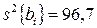 ;
; 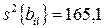 ;
; 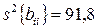 .
.
Определяем доверительные интервалы для коэффициентов:
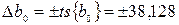 ;
; 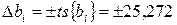 ;
;
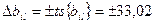 ;
; 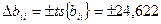 .
.
Таблица 4.10
Матрица планирования и результаты опытов
| № опыта | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | 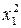
| 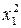
| 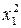
| y,H (PT) |
| + | + | + | + | + | + | + | + | + | + | ||
| + | + | + | – | + | – | – | + | + | + | ||
| + | + | – | + | – | + | – | + | + | + | ||
| + | + | – | – | – | – | + | + | + | + | ||
| + | – | + | + | – | – | + | + | + | + | ||
| + | – | + | – | – | + | – | + | + | + | ||
| + | – | – | + | + | – | – | + | + | + | ||
| + | – | – | – | + | + | + | + | + | + | ||
| + | +1,682 | 2,829 | |||||||||
| + | –1,682 | 2,829 | |||||||||
| + | +1,682 | 2,829 | |||||||||
| + | –1,682 | 2,829 | |||||||||
| + | +1,682 | 2,829 | |||||||||
| + | –1,682 | 2,829 | |||||||||
| + | |||||||||||
| + | |||||||||||
| + | |||||||||||
| + | |||||||||||
| + | |||||||||||
| + |
Таблица 4.11
Вспомогательная таблица для расчета 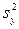
| Номер опыта | yu | 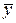
| 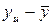
| 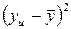
| 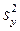
|
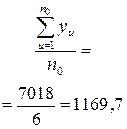
| –51,7 | 2672,89 | 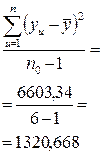
| ||
| –29,7 | 882,09 | ||||
| –9,7 | 1624,09 | ||||
| 40,3 | 412,09 | ||||
| 20,3 | 918,09 | ||||
| 30,3 | |||||
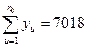
| 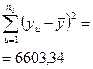
|
где t=2,57 – табличное значение критерия Стьюдента при 5%-ном уровне значимости и числе степеней свободы f=5.
Коэффициенты b1, b12, b22, b33,. меньше доверительных интервалов, поэтому их можно признать статистически незначимыми и исключить из уравнения регрессии.
После исключения незначимых коэффициентов уравнение (4.11) принимает вид
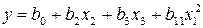 (4.12)
(4.12)
Так как среди незначимых оказались коэффициенты при квадратичных членах, то коэффициенты уравнения (4.12) были пересчитаны с использованием метода наименьших квадратов.
Для пересчета коэффициентов уравнения (4.12) составили систему нормальных уравнений [3]:
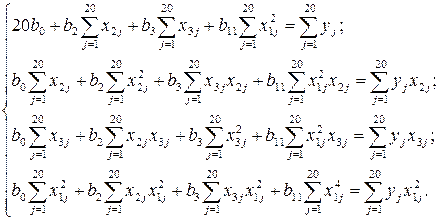
Определили суммы, входящие в систему нормальных уравнений
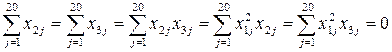 ;
;
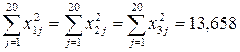 ;
; 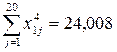 .
.
Суммы, находящиеся в правых частях уравнений, вычислены раньше. После подстановки значений сумм система нормальных уравнений приняла вид 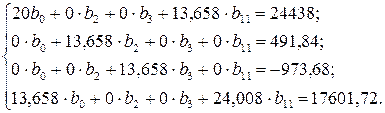
Решив систему нормальных уравнений, определим значения коэффициентов
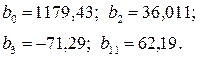
В результате использования ротатабельного планирования второго порядка получили следующее уравнение регрессии:
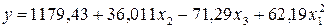 (4.13)
(4.13)
Проверка гипотезы адекватности модели (4.13) показала, что модель адекватна при 5%-ном уровне значимости, так как расчетное значение F – критерия меньше табличного.
Вычисленные по уравнению (4.13) значения y отличаются от экспериментальных на величины, не превышающие ошибку опыта. Кодированные значения факторов связаны с натуральными следующими зависимостями:
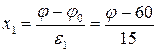 ;
;
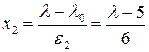 ;
;
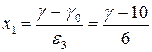 ,
,
где φо, λо, γо – основные уровни факторов в натуральных выражениях; ε1 ε2, ε3 – интервалы варьирования факторов.
Переходя от кодированных x1 x2, x3 значений факторов к натуральным φ, λ, γ, получим зависимость максимальной тангенциальной составляющей силы резания от элементов геометрии зуба торцовой фрезы:
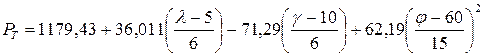 .
.
После преобразования
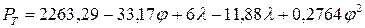 H. (4.14)
H. (4.14)
Уравнение (4.14) адекватно, поэтому его можно использовать как интерполяционную формулу для вычисления величины Рт.
При конструировании торцовых фрез для обработки высокопрочного чугуна уравнение (4.14) может быть использовано для установления рациональных значений элементов геометрии зуба.
4.4. Составление композиционного плана проведения экспериментов при анализе параметров процесса шлифования
Установление зависимости выходных параметров шлифования от входных факторов необходимо для прогнозирования и управления процессом. С этой целью было проведено исследование.
Процессы шлифования описываются, как правило, степенными эмпирическими зависимостями.
В технических исследованиях широко применяются методы планирования экстремальных экспериментов, при использовании которых предполагается степенная эмпирическая зависимость процесса [1-3]. Логарифмирование этой зависимости позволяет получить исходный полином первой степени. Математическая обработка результатов эксперимента, поставленного по факторному плану, дает возможность определить коэффициенты этого полинома и тем самым установить зависимость процесса применительно к конкретным условиям.
Например, предполагая степенную зависимость эффективной мощности шлифования Nэф от глубины шлифования t, подачи S, скорости резания Vкр, и скорости детали Vдет.
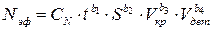 ,
,
логарифмируем это выражение:
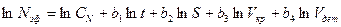 .
.
Произведя замену переменных
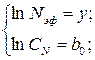
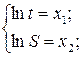
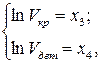
получим исходный полином первой степени:
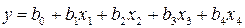 .
.
В этом полиноме натуральные значения переменных факторов t, S, Vкр, Vдет находятся под знаком логарифма, а коэффициенты регрессии являются предметом поиска.
Кодирование переменных, производимое по формуле:
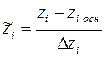 , (4.15)
, (4.15)
где 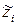 – кодированное значение переменного фактора;
– кодированное значение переменного фактора;
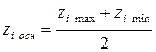 ; (4.16)
; (4.16)
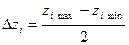 ; (4.17)
; (4.17)
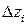 – интервал варьирования в натуральных величинах переменного фактора;
– интервал варьирования в натуральных величинах переменного фактора;
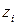 – текущее натуральное значение переменного фактора;
– текущее натуральное значение переменного фактора;
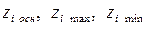 – соответственно среднее, максимальное и минимальное значения переменного фактора,
– соответственно среднее, максимальное и минимальное значения переменного фактора,
Значение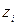 вносит существенные погрешности в план эксперимента, ибо натуральные переменные факторы в исходном полиноме находятся под знаком логарифма.
вносит существенные погрешности в план эксперимента, ибо натуральные переменные факторы в исходном полиноме находятся под знаком логарифма.
Подставляя в формулы (4.16) и (4.17) вместо переменных 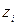 значения
значения 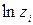 , а затем полученные выражения – в формулу (4.15) и произведя некоторые преобразования, получим формулу для кодирования переменных, находящихся под знаком логарифма в исходном полиноме:
, а затем полученные выражения – в формулу (4.15) и произведя некоторые преобразования, получим формулу для кодирования переменных, находящихся под знаком логарифма в исходном полиноме:
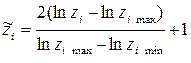 . (4.18)
. (4.18)
Из формулы (4.18) следует, что натуральное значение переменного фактора, находящегося на основном уровне плана, т.е. в случае 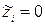 и
и 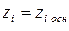 , должно быть
, должно быть 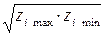 , а не будет равно полусумме максимального и минимального натуральных значений фактора, как при факторном планировании без логарифмирования (характерная ошибка при использовании степенных моделей).
, а не будет равно полусумме максимального и минимального натуральных значений фактора, как при факторном планировании без логарифмирования (характерная ошибка при использовании степенных моделей).
При исследовании "почти стационарной области" процесса планы эксперимента усложняются, становятся композиционными, включающими "звездные точки"; порядок этих планов увеличивается. Плечо "звездной точки"
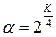 ,
,
где K – число переменных факторов.
Предельные натуральные значения фактора определяются возможностями оборудования, приборов. Поэтому, используя композиционные планы второго и более высокого порядков, нужно учитывать, что натуральные значения переменного фактора в "звездных точках" не должны превышать предельных значений, обеспечиваемых оборудованием.
По принятым натуральным предельным значениям фактора 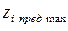 и
и 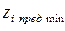 в "звездных точках" α можно рассчитать натуральные значения фактора в точках плана (уровнях):
в "звездных точках" α можно рассчитать натуральные значения фактора в точках плана (уровнях):
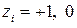 и –1.
и –1.
Преобразовав формулу (4.18) и далее потенцируя выражение, подучим зависимость натурального значения фактора 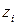 от
от 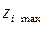 , соответствующего кодированному значению
, соответствующего кодированному значению 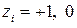 , и
, и 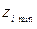 , соответствующего кодированному значению
, соответствующего кодированному значению 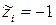 :
:
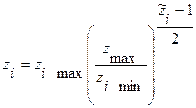 (4.19)
(4.19)
Из зависимости (4.19) видно, что предельные значения 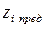 при
при 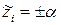 будут:
будут:
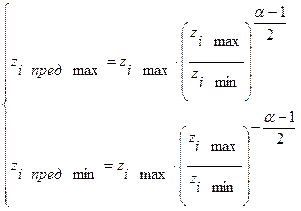 ;
;
Решая совместно эту систему уравнений получим три основные формулы:
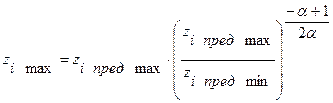 ;
;
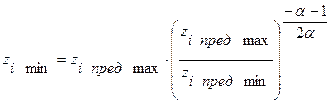 ;
;
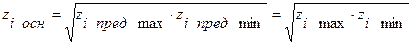 .
.
Эти формулы позволяют по предельным натуральным значениям факторов, находящихся на уровнях 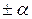 определять натуральные значения факторов на уровнях +1, 0, -1 и при этих значениях факторов ставить эксперименты по композиционным планам второго и более высокого порядков. Эти натуральные значения факторов обеспечивают получение в кодированном виде плана, обладающего свойствами ортогональности и рототабельности.
определять натуральные значения факторов на уровнях +1, 0, -1 и при этих значениях факторов ставить эксперименты по композиционным планам второго и более высокого порядков. Эти натуральные значения факторов обеспечивают получение в кодированном виде плана, обладающего свойствами ортогональности и рототабельности.
Дата добавления: 2019-10-16; просмотров: 748;
