Исследование температуры, возникающей в зоне резания
Рассмотрим методику получения зависимости температуры 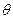 резания от скорости υ, подачи s и глубины резания t при обработке точением стали 20 цельными проходными резцами из быстрорежущей стали Р18 [3].
резания от скорости υ, подачи s и глубины резания t при обработке точением стали 20 цельными проходными резцами из быстрорежущей стали Р18 [3].
Эмпирические температурные зависимости часто представляют уравнениями регрессии вида
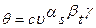 . (4.33)
. (4.33)
Уравнение (4.33) после логарифмирования получит вид
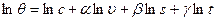 . (4.34)
. (4.34)
Решено представить результаты эксперимента полиномом второй степени:
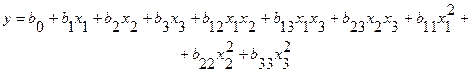 , (4.35)
, (4.35)
где 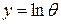 ; θ – температура;
; θ – температура; 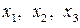 – кодированные значения факторов υ, s, t.
– кодированные значения факторов υ, s, t.
В качестве плана эксперимента использовали центральный композиционный ротатабельный план второго порядка.
Кодирование независимых переменных производили с помощью соотношения (4.23).
Принятые в исследовании уровни факторов указаны в табл.4.14.
Таблица 4.14
Уровни факторов
| Уровни факторов | υ,м/с . | x1 | s, мм/об | x2 | t, мм | х3 |
| Верхнее «звездное плечо»: | 0,725 | 1,682 | 0,463 | 1,682 | 1,49 | 1,682 |
| Верхний уровень | 0,454 | 0,26 | 1,04 | |||
| Основной уровень | 0,229 | 0,17 | 0,61 | |||
| Нижний уровень | 0,115 | –1 | 0,11 | –1 | 0,36 | –1 |
| Нижнее «звездное плечо» | 0,072 | –1,682 | 0,082 | –1,682 | 0,25 | –1,682 |
Формулы преобразования натурных значений факторов кодированные в данном случае имеют вид [3]
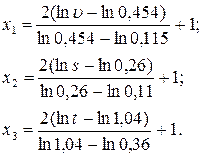 (4.36)
(4.36)
Матрица планирования и результаты опытов представлены в табл.4.15.
В результате расчетов коэффициентов получено следующее уравнение регрессии:
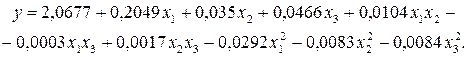 (4.37)
(4.37)
Дисперсию воспроизводимости вычисляли по результатам шести опытов в центре плана 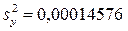 .
.
Дисперсии коэффициентов уравнения регрессии, полученные в режиме расчетов,
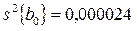 ;
;
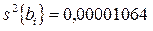 ;
;
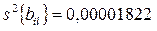 ;
;
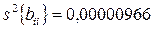 .
.
Доверительные интервалы коэффициентов при 5.% -ном уровне значимости:
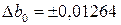 ;
;
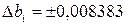 ;
;
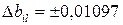 ;
;
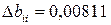 .
.
Коэффициенты b12, b13, b23 по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии.
После исключения незначимых коэффициентов уравнение (4.37) получило вид
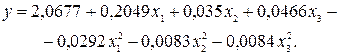 (4.38)
(4.38)
Проверка гипотезы адекватности модели, представленной уравнением (4.38), показала, что модель адекватна при 5%-ном уровне значимости, так как FP<FT.
Таблица 4.15
Матрица планирования и результаты опытов
| Номер опыта | x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | 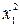
| 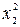
| 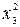
| y |
| + | – | – | – | + | + | + | + | + | + | 1,6879 | |
| + | + | – | – | – | – | + | + | + | + | 2,0777 | |
| + | – | + | – | – | + | – | + | + | + | 1,8499 | |
| + | + | + | – | + | – | – | + | + | + | 2,2837 | |
| + | – | – | + | + | – | – | + | + | + | 1,7787 | |
| + | + | – | + | – | + | – | + | + | + | 2,1677 | |
| + | – | + | + | – | – | + | + | + | + | 1,9479 | |
| + | + | + | + | + | + | + | + | + | + | 2,3801 | |
| + | –1,682 | 2,829 | 1,6391 | ||||||||
| + | +1,682 | 2,829 | 2,3311 | ||||||||
| + | –1,682 | 2,829 | 1,8868 | ||||||||
| + | +1,682 | 2,829 | 2,2016 | ||||||||
| + | –1,682 | 2,829 | 1,9652 | ||||||||
| + | +1,682 | 2,829 | 2,1226 | ||||||||
| + | 2,0551 | ||||||||||
| + | 2,0734 | ||||||||||
| + | 2,0743 | ||||||||||
| + | 2,0568 | ||||||||||
| + | 2,0608 | ||||||||||
| + | 2,0858 |
Это свидетельствует о том, что исследуемый процесс не может быть описан уравнением (4.33). Уравнение (4.38) для рассматриваемой области изменения факторов дает возможность предложить другую модель процесса. Эту модель получим, подставив в уравнение (4.38) вместо кодированных натуральные значения факторов, используя для этого соотношения (4.36).
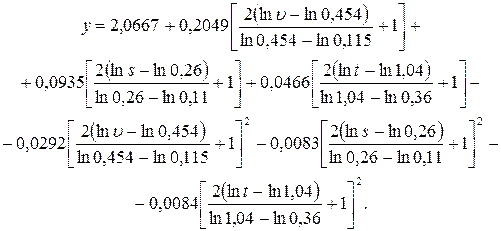
После преобразования получена зависимость
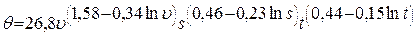 , (4.39)
, (4.39)
которая позволяет определять температуру резания в достаточно широком диапазоне изменения режимов резания при обработке точением стали 20. По уравнению (4.39) может быть построена номограмма, которая позволит в практических условиях определять температуру резания при выбранных значениях элементов режима резания.
Рассмотренные в настоящем учебном пособии теоретические вопросы, связанные с планированием и реализацией многофакторных экспериментов, приведенные конкретные примеры применения изложенной методологии применительно к различным процессам механической обработки деталей способствуют освоению читателями процедуры постановки, проведения многофакторных экспериментальных исследований, статистической обработки результатов и проверки полученных моделей на адекватность, что несомненно повысит научно – технический уровень проводимых исследований.
Для реализации экстремальных планируемых многофакторных экспериментов необходимо использовать статистические данные, содержащиеся в таблицах 1-5, приведенных в приложении.
СПИСОК ЛИТЕРАТУРЫ
1.Кане М. М. Исследования и изобретательство в машиностроении /И. Л. Барщай, Г. Я. Беляев, О. Г. Девойно// Под общ. ред. М. М. Кане.-Мн.: УП Технопринт, 2003.-237с, ISBN 985-464-479-0
2.Пижурин А. А., Пижурин А. А. Основы научных исследований в деревообработке. – М: МГУЛ, 2005.-ЗО6с.
З.Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов.– М.: Машиностроение, 1981.- 184с., ББК 34.5 С72.
Дата добавления: 2019-10-16; просмотров: 593;
