Касательная плоскость и нормаль к поверхности
Пусть поверхность 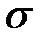 определена в некоторой окрестности точки
определена в некоторой окрестности точки 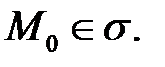
Определение 1.Геометрическое место касательных прямых, проведенных к всевозможным гладким кривым
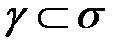 , проходящим через точку
, проходящим через точку 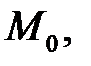 называется касательной плоскостью к поверхности
называется касательной плоскостью к поверхности 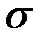 в точке
в точке 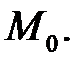 Прямая
Прямая 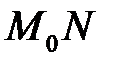 , проходящая через точку
, проходящая через точку 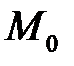 перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности
перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности 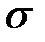 в точке
в точке 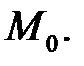
Пусть поверхность 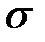 задана уравнением
задана уравнением 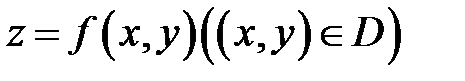 и пусть кривая
и пусть кривая 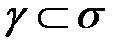 проходит через точку
проходит через точку 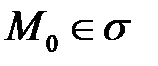 и имеет касательную в этой точке. Зададим эту кривую параметрически уравнениями
и имеет касательную в этой точке. Зададим эту кривую параметрически уравнениями 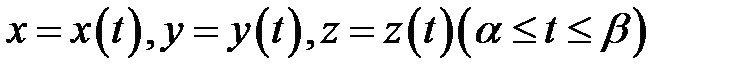 и пусть точка
и пусть точка 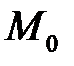 соответствует параметру
соответствует параметру 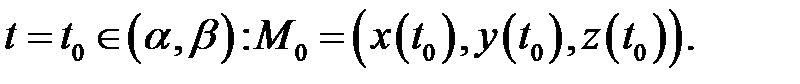 Тогда вектор
Тогда вектор 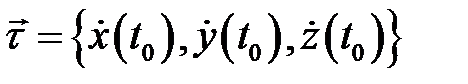 является касательным вектором к кривой
является касательным вектором к кривой 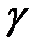 в точке
в точке 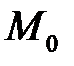 . Так как кривая лежит на поверхности
. Так как кривая лежит на поверхности 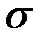 , то выполняется тождество
, то выполняется тождество 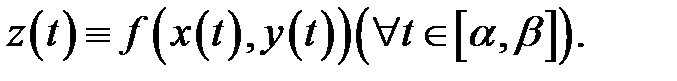 Пусть
Пусть 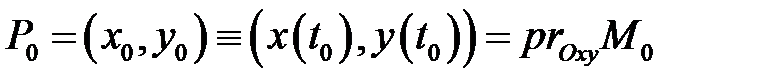 – проекция точки
– проекция точки 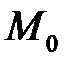 на плоскость
на плоскость 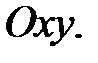 Предположим, что функция
Предположим, что функция 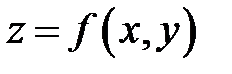 дифференцируема в точке
дифференцируема в точке 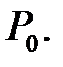 Тогда сложную функцию
Тогда сложную функцию 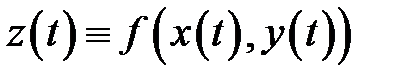 можно дифференцировать по
можно дифференцировать по 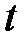 в точке
в точке 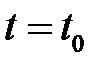 . Сделав это, получим
. Сделав это, получим
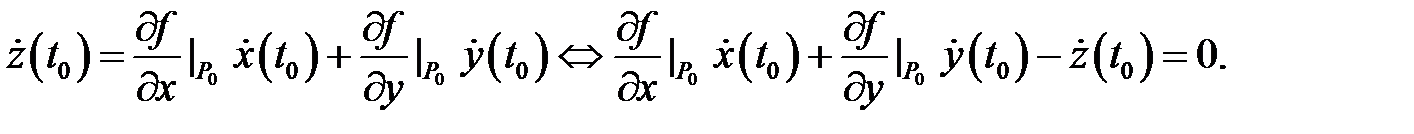
Это равенство показывает, что вектор 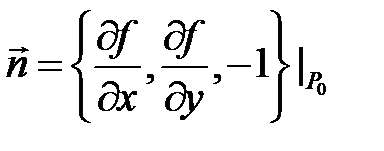 ортогонален касательному вектору
ортогонален касательному вектору
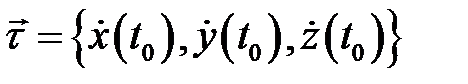 к кривой
к кривой 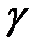 . Нетрудно видеть, что это утверждение верно для любой гладкой кривой
. Нетрудно видеть, что это утверждение верно для любой гладкой кривой 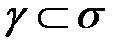 , проходящей через точку
, проходящей через точку 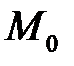 , поэтому вектор
, поэтому вектор 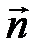 перпендикулярен к касательной плоскости
перпендикулярен к касательной плоскости 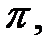 проходящей через точку
проходящей через точку 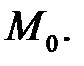 Пусть
Пусть 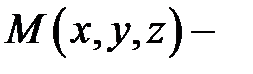 произвольная точка плоскости
произвольная точка плоскости 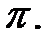 Из аналитической геометрии вытекает, что уравнение этой плоскости имеет вид
Из аналитической геометрии вытекает, что уравнение этой плоскости имеет вид
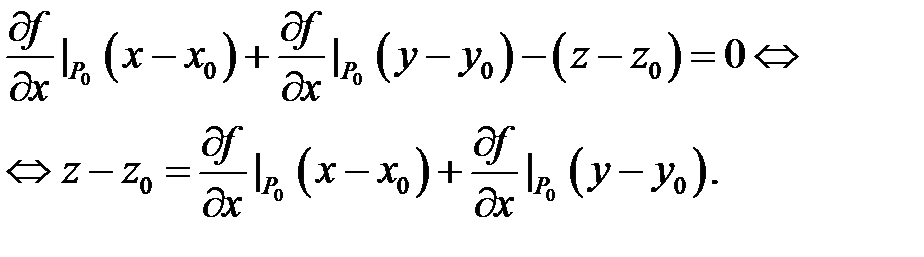
Мы приходим к следующему утверждению.
Теорема 1. Пусть поверхность 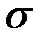 задана уравнением
задана уравнением 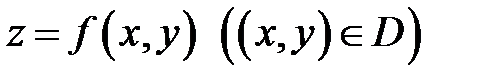 и пусть функция
и пусть функция 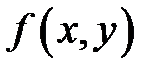 дифференцируема в точке
дифференцируема в точке 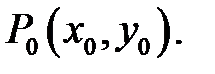 Тогда в точке
Тогда в точке 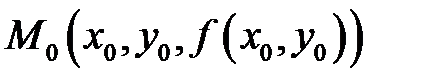 поверхность
поверхность 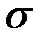 имеет касательную плоскость, уравнение которой записывается в виде
имеет касательную плоскость, уравнение которой записывается в виде
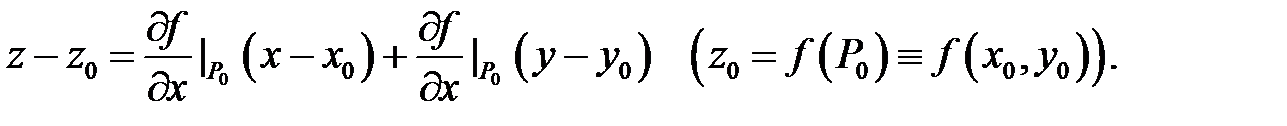
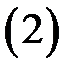
Если поверхность 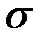 задана неявно уравнением
задана неявно уравнением 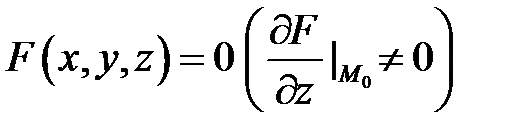 , то уравнение касательной плоскости к ней в точке
, то уравнение касательной плоскости к ней в точке 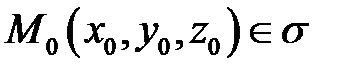 имеет вид
имеет вид
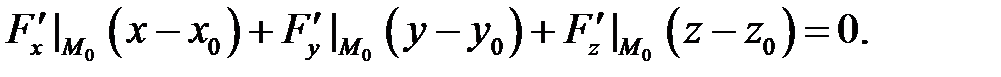
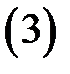
Заметим, что уравнение (3) выводится из уравнения (2), если в него подставить частные производные функции 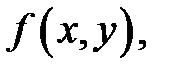 вычисляемые по ранее полученным формулам
вычисляемые по ранее полученным формулам
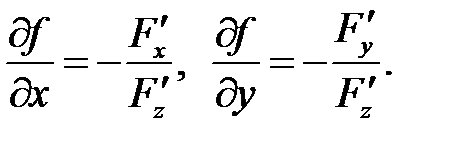
Учитывая, что вектор 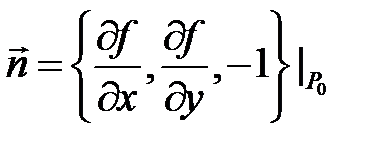 является направляющим вектором нормали к поверхности
является направляющим вектором нормали к поверхности 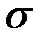 в точке
в точке 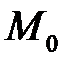 , то уравнение нормали будет иметь вид[4]
, то уравнение нормали будет иметь вид[4]
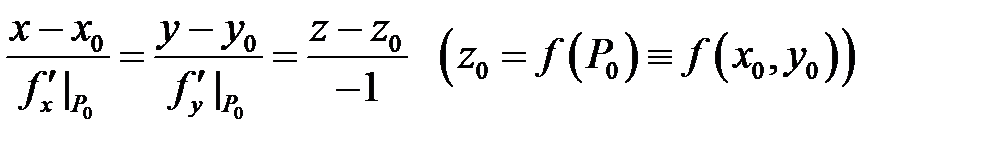
в случае явного задания 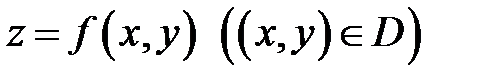 поверхности
поверхности 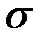 и
и
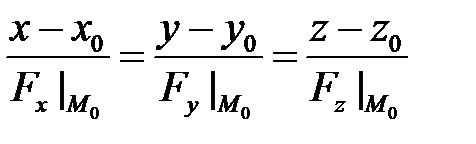
в случае неявного задания 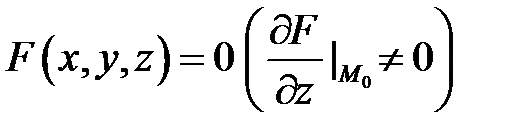 поверхности
поверхности 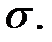
В уравнении (2) величина 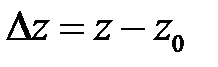 является приращением аппликаты касательной плоскости, а величины
является приращением аппликаты касательной плоскости, а величины 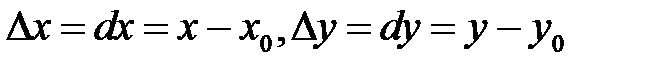 – приращениями аргументов, поэтому равенство (2) можно записать так:
– приращениями аргументов, поэтому равенство (2) можно записать так: 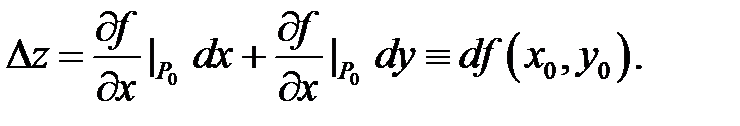 Отсюда вытекает следующий геометрический смысл дифференциала: дифференциал
Отсюда вытекает следующий геометрический смысл дифференциала: дифференциал 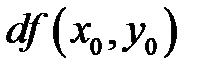 функции
функции 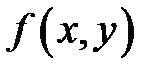 в точке
в точке 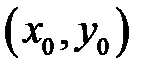 равен приращению аппликаты касательной плоскости при переходе
равен приращению аппликаты касательной плоскости при переходе 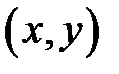 из точки
из точки 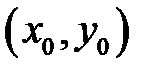 в точку
в точку 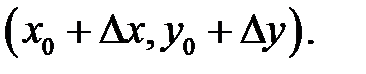
Дата добавления: 2017-03-29; просмотров: 1146;
