Скалярное поле. Производная скалярного поля по направлению, связь с градиентом
Если в некоторой области 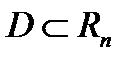 задана функция
задана функция  то говорят, что в
то говорят, что в 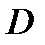 задано скалярное поле. Например,
задано скалярное поле. Например, 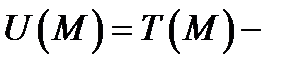 температура тела
температура тела 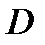 в точке
в точке 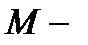 является скалярным полем. Будем, как и прежде, рассматривать случай
является скалярным полем. Будем, как и прежде, рассматривать случай 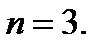 Пусть
Пусть  фиксированная точка области
фиксированная точка области 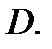 Сместимся из точки
Сместимся из точки 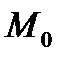 в точку
в точку 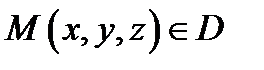 по направлению
по направлению 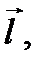 определяемым единичным вектором
определяемым единичным вектором 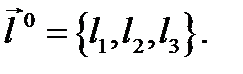 Введем следующее понятие.
Введем следующее понятие.
Определение 2.Если существует конечный предел
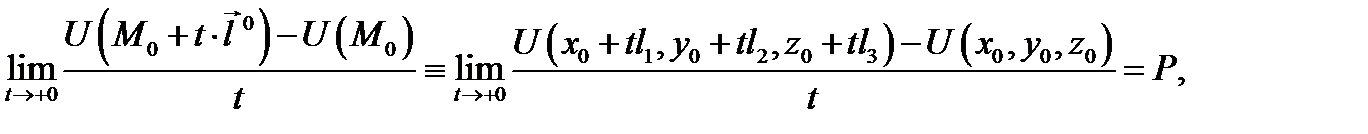
то его называют производной поля
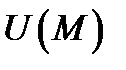 в точке
в точке 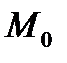 по направлению
по направлению 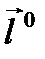 и обозначают
и обозначают 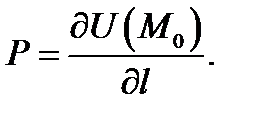
Производная 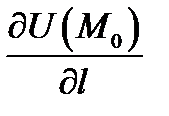 показывает скорость изменения поля
показывает скорость изменения поля 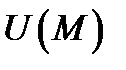 в точке
в точке 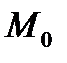 в направлении
в направлении 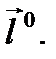 Введем ещё одно понятие.
Введем ещё одно понятие.
Определение 3 .Градиентом скалярного поля 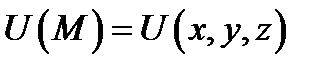 в точке
в точке 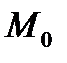 называется вектор
называется вектор


Следующая теорема устанавливает связь между градиентом и производной поля по направлению.
Теорема 8.Если поле 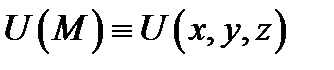 дифференцируемо в точке
дифференцируемо в точке 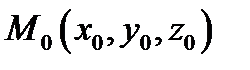 и
и 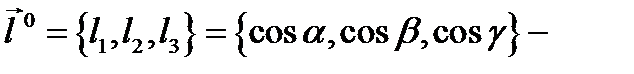 единичный вектор направления
единичный вектор направления  то
то

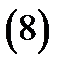
Доказательствопроведем для плоского скалярного поля.Рассмотрим функцию 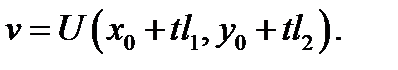 По определению 2 имеем
По определению 2 имеем 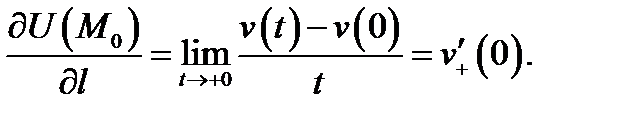 Так как функция
Так как функция  дифференцируема в точке
дифференцируема в точке 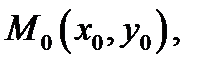 а функции
а функции  дифференцируемы в точке
дифференцируемы в точке 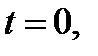 то сложная функция
то сложная функция 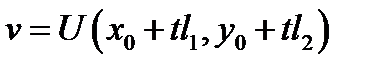 дифференцируема в точке
дифференцируема в точке 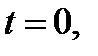 причем
причем

Теорема доказана.
Данное нами определение градиента зависит от выбора системы координат. Инвариантное определение градиента следующее: градиентом поля  в точке
в точке  называется такой вектор
называется такой вектор  , проекция которого на произвольное направление
, проекция которого на произвольное направление 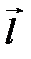 в этой точке совпадает с производной поля
в этой точке совпадает с производной поля  по направлению
по направлению 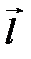 в точке
в точке  т.е.
т.е. 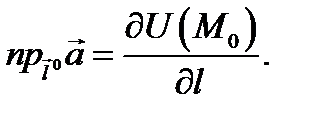
Если выбрать систему координат с ортами 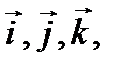 то
то 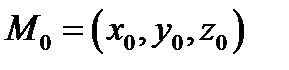 и взять
и взять 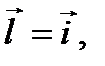 то по теореме 8 получаем, что
то по теореме 8 получаем, что
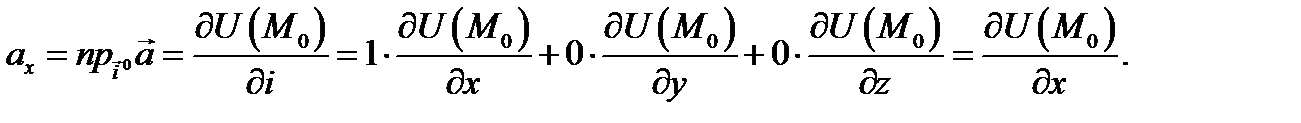
И аналогично, 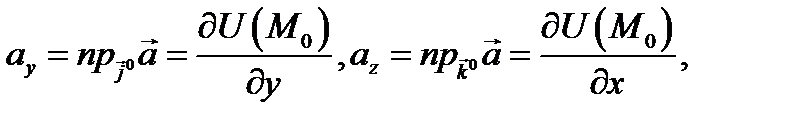 и мы получаем ранее данное определение градиента:
и мы получаем ранее данное определение градиента: 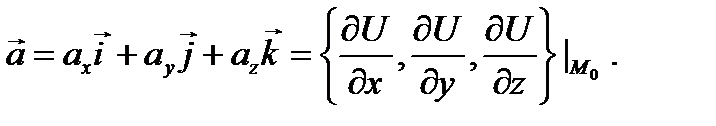 Нетрудно установить следующие свойства градиента.
Нетрудно установить следующие свойства градиента.
 Производная по направлению
Производная по направлению 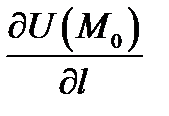 имеет наибольшее значение в направлении
имеет наибольшее значение в направлении
 При этом
При этом 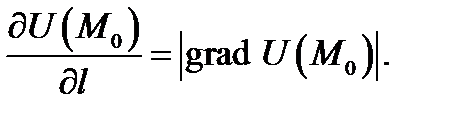
 Градиент
Градиент 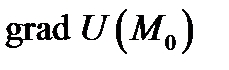 направлен по нормали к поверхности уровня
направлен по нормали к поверхности уровня 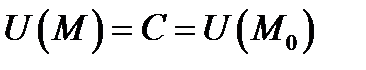 в сторону наибольшего изменения поля
в сторону наибольшего изменения поля 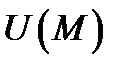 в точке
в точке 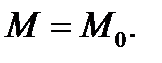
Лекция 3. Касательная плоскость и нормаль к поверхности. Локальный экстремум функции нескольких переменных, необходимое условие экстремума. Достаточные условия существования экстремума. Наибольшее и наименьшее значения функции на замкнутом ограниченном множестве. Условный экстремум и метод множителей Лагранжа
Прежде чем перейти к изложению следующего раздела, отметим, что кривую в пространстве 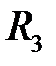 можно задать системой уравнений
можно задать системой уравнений
 .
. 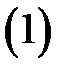
Действительно, при изменении параметра
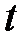 на отрезке
на отрезке 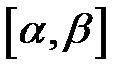 точка
точка 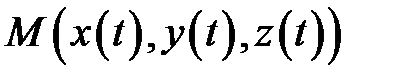 описывает в
описывает в 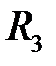 некоторую кривую
некоторую кривую  При этом кривая
При этом кривая 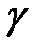 называется непрерывной, если все функции непрерывны на отрезке
называется непрерывной, если все функции непрерывны на отрезке 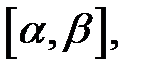 и
и  называется гладкой кривой, если производные
называется гладкой кривой, если производные 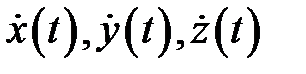 непрерывны на указанном отрезке. Точка
непрерывны на указанном отрезке. Точка 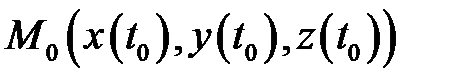 называется неособой, если
называется неособой, если 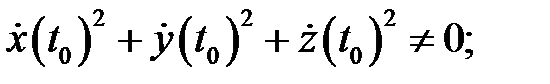 в противном случае (т.е. в случае
в противном случае (т.е. в случае  )точка
)точка 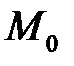 называется особой. Нетрудно показать, что вектор
называется особой. Нетрудно показать, что вектор 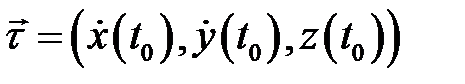 является касательным вектором к кривой
является касательным вектором к кривой 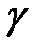 в точке
в точке 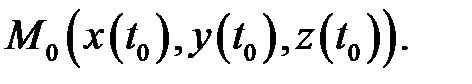
Дата добавления: 2017-03-29; просмотров: 717;
