Наибольшее и наименьшее значения функции
Так же, как и для функции одной переменной, для функций многих переменных имеет место следующее утверждение.
Теорема Вейерштрасса.Если функция 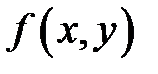 непрерывна на замкнутом ограниченном множестве [6]
непрерывна на замкнутом ограниченном множестве [6] 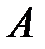 , то она ограничена на нём и достигает на нём своих наибольшего и наименьшего значений, т.е. существуют точки
, то она ограничена на нём и достигает на нём своих наибольшего и наименьшего значений, т.е. существуют точки 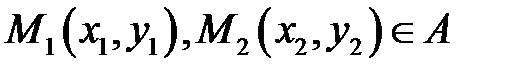 такие, что
такие, что
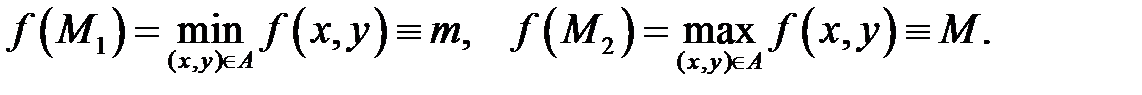
Для нахождения 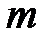 и
и 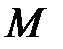 поступают следующим образом:
поступают следующим образом:
1) Находят сначала все критические точки функции 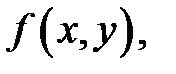 лежащие внутри
лежащие внутри 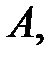 (т.е. в области
(т.е. в области 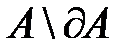 ) и вычисляют значения функции
) и вычисляют значения функции 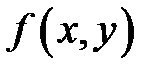 в этих критических точках;
в этих критических точках;
2) Вычисляют наибольшее и наименьшее значения на границе 
3) Среди всех найденных значений выбирают наименьшее и наибольшее. Они и будут равны 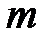 и
и 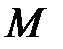 соответственно.
соответственно.
Пример 1.Найти наибольшее и наименьшее значения функции 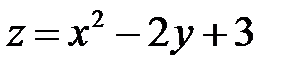 в области
в области
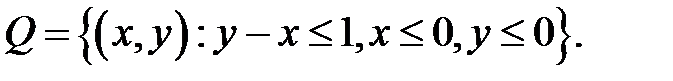
Решение.Данная область является треугольником с вершинами 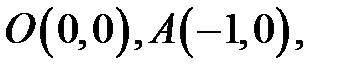
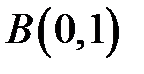 стороны которого расположены на прямых
стороны которого расположены на прямых 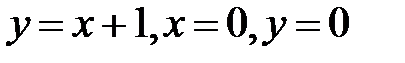 (рис. 1).
(рис. 1).
1) Найдем стационарные точки внутри области. Вычислим частные производные функции и приравняем их нулю:
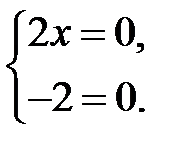
Полученная система не имеет решения. Следовательно, критических точек внутри области нет.
1) Найдем критические точки внутри области. Вычислим частные
производные функции и приравняем их нулю:
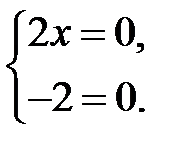
Полученная система не имеет решения. Следовательно, критических точек внутри области нет.
2) Найдем стационарные точки на стороне AO . Координаты точек, лежащих на AO удовлетворяют условиям
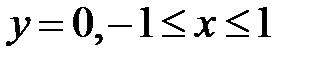 . Тогда рассматриваемая функция принимает вид
. Тогда рассматриваемая функция принимает вид 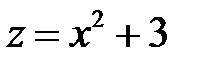 . Критическая точка определяется из условия
. Критическая точка определяется из условия

Вычислим значение функции в найденной точке 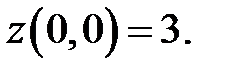
3) Рассмотрим точки, лежащие на стороне OB. Их координаты удовлетворяют условиям 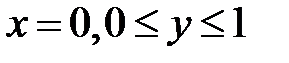 . При этом имеем
. При этом имеем 
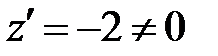 , то есть на стороне OB критических точек нет.
, то есть на стороне OB критических точек нет.
4) Найдем критические точки на стороне AB . Здесь
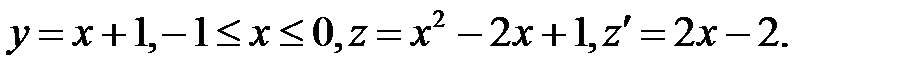
Из уравнения 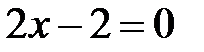 находим критическую точку
находим критическую точку 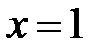 . Однако она не принадлежит рассматриваемому отрезку.
. Однако она не принадлежит рассматриваемому отрезку.
5) Найдем значения функции в вершинах треугольника 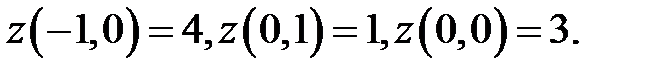
Так как единственная критическая точка совпала с вершиной треугольника O(0,0) , выберем
наибольшее и наименьшее из этих значений. Итак, функция принимает наибольшее значение
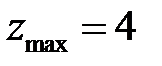 в точке
в точке  наименьшее значение
наименьшее значение 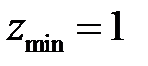 в точке
в точке 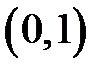 .
.
Дата добавления: 2017-03-29; просмотров: 1001;
