Тройной интеграл, его свойства и вычисление
Пусть 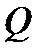 – замкнутая ограниченная (кубируемая) область (тело) в
– замкнутая ограниченная (кубируемая) область (тело) в 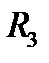 и функция
и функция 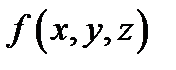 определена в
определена в  . Произведем разбиение
. Произведем разбиение 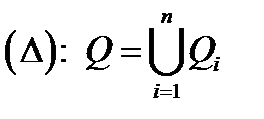 этой области на частичные подобласти
этой области на частичные подобласти 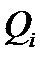 с помощью конечного числа непрерывных поверхностей. Обозначим через
с помощью конечного числа непрерывных поверхностей. Обозначим через 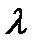 диаметр разбиения
диаметр разбиения 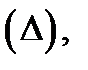 т.е. число
т.е. число  Возьмём произвольно точку
Возьмём произвольно точку 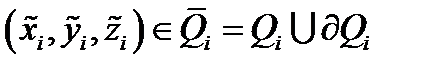 и составим интегральную сумму
и составим интегральную сумму 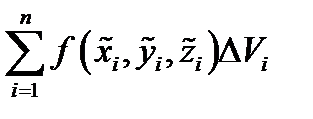 (где
(где 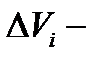 объём области
объём области 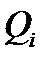 ).
).
Определение 2.Если существует конечный предел интегральных сумм: 
 и если этот предел не зависит от вида разбиения
и если этот предел не зависит от вида разбиения 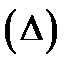 и выбора точек
и выбора точек  то его называют двойным интегралом от функции
то его называют двойным интегралом от функции 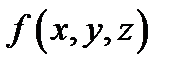 по области
по области 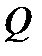 и обозначают
и обозначают 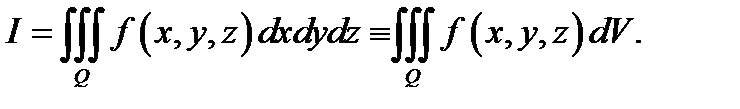 При этом функция
При этом функция 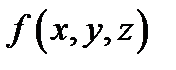 называется интегрируемой в области
называется интегрируемой в области 
Механический смысл тройного интеграла.Если 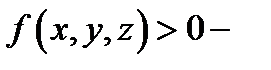 плотность тела
плотность тела 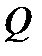 в точке
в точке 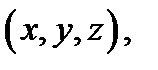 то произведение
то произведение  приближенно равно массе тела
приближенно равно массе тела 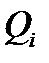 , а интегральная сумма
, а интегральная сумма 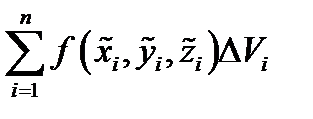 приближенно равна массе всего тела
приближенно равна массе всего тела 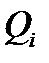 , т.е.
, т.е. 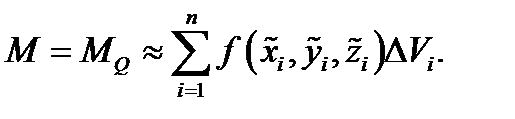 Ясно, что это равенство будет тем точнее, чем мельче разбиение
Ясно, что это равенство будет тем точнее, чем мельче разбиение 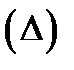 , и при
, и при 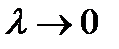 оно становится точным:
оно становится точным:

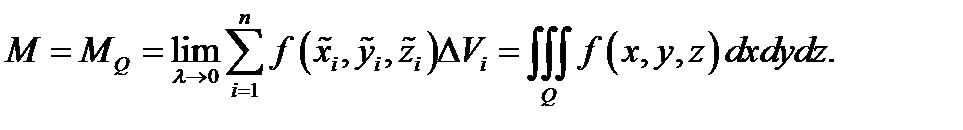
Таким образом, тройной интеграл по телу 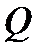 от плотности
от плотности 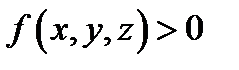 равен массе тела
равен массе тела 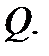
Тройные интегралы обладают свойствами, аналогичными свойствам двойных интегралов. Сформулируем их, предполагая, что  замкнутая ограниченная кубируемая область в
замкнутая ограниченная кубируемая область в 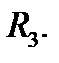
10) (линейность) Если функции 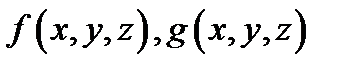 интегрируемы в
интегрируемы в 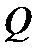 , то и любая их линейная комбинация
, то и любая их линейная комбинация 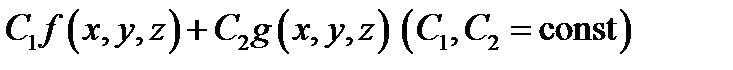 также интегрируема в
также интегрируема в 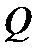 , причем имеет место равенство
, причем имеет место равенство
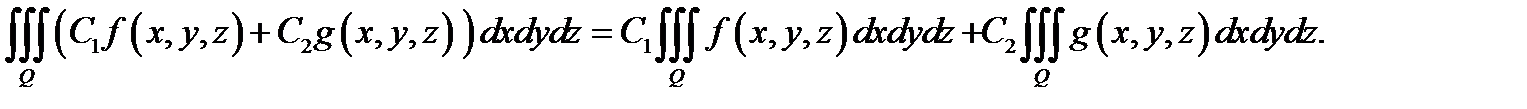
20) (аддитивность) Если область 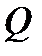 разбита на две непересекающиеся подобласти
разбита на две непересекающиеся подобласти 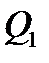 и
и  с помощью непрерывной поверхности и если функция
с помощью непрерывной поверхности и если функция  интегрируема в
интегрируема в 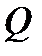 , то она интегрируема и в каждой из областей
, то она интегрируема и в каждой из областей 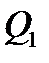 и
и  (и наоборот). При этом имеет место равенство
(и наоборот). При этом имеет место равенство 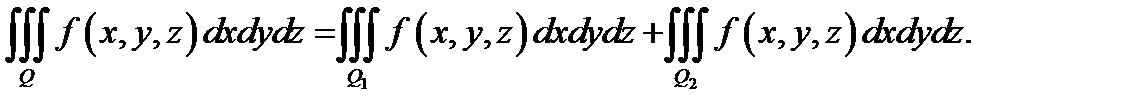
30) (монотонность) Если функции 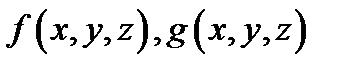 интегрируемы в
интегрируемы в  и имеет место неравенство
и имеет место неравенство 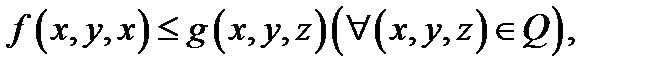 то
то
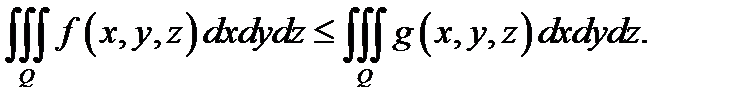
40) Если функция 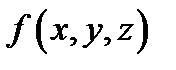 интегрируема в
интегрируема в 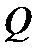 и имеют место неравенства
и имеют место неравенства
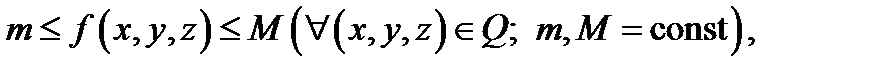
то
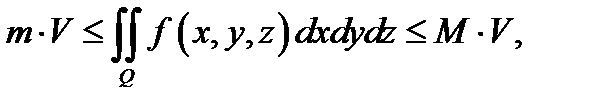
где  объём области
объём области 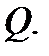
50) (теорема о среднем) Если функция 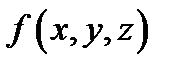 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 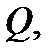 то существует точка
то существует точка 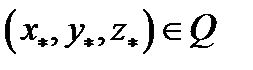 такая, что
такая, что

И, наконец, отметим, что любая непрерывная и кусочно непрерывная в замкнутой ограниченной (кубируемой) области  функция интегрируема в
функция интегрируема в 

Теорема 3(Фубини).Если 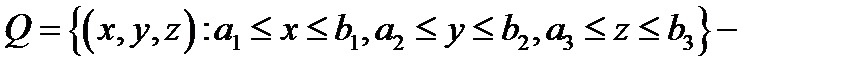 параллелепи-
параллелепи-
пед и если функция 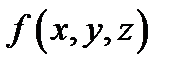 кусочно непрерывна в
кусочно непрерывна в 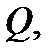 то
то
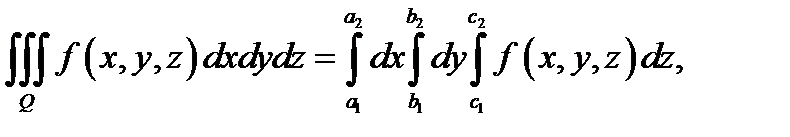
причем здесь порядок интегрирования может быть изменён как-угодно.
Теорема 4(вычисление тройного интеграла в криволинейной области). Если  имеет вид
имеет вид 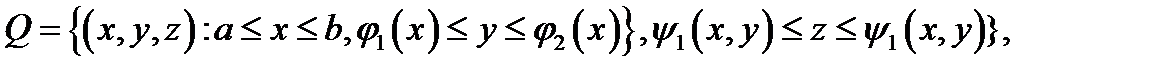
где функции 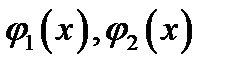 непрерывны на отрезке
непрерывны на отрезке  а функции
а функции 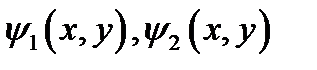 непрерывны в области
непрерывны в области 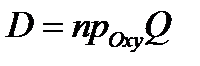 и если функция
и если функция 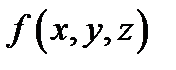 непрерывна в
непрерывна в 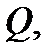 то
то
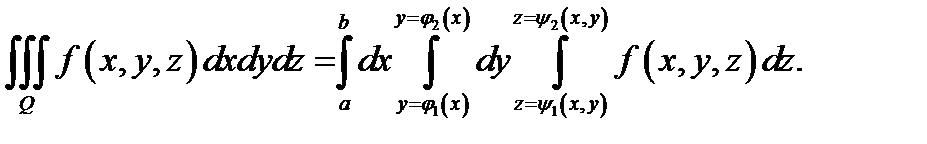

Доказательство этой теоремы фактически повторяет доказательство теоремы 2 и опирается на теорему Фубини. Заметим, что если область 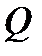 является правильной в направлении всех трех осей, то можно изменять порядок интегрирования.
является правильной в направлении всех трех осей, то можно изменять порядок интегрирования.
Пример 4 (Кузнецов Л.А. Типовые расчеты). Вычислить интеграл 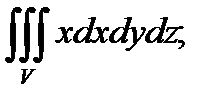 где
где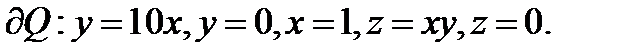
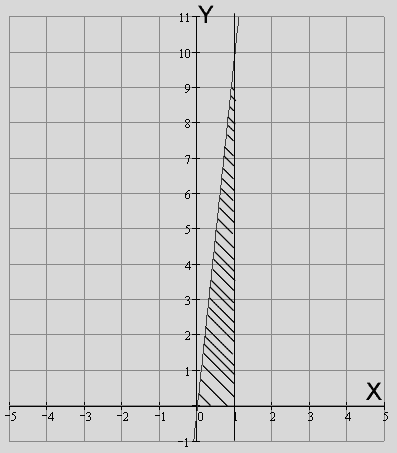 Решение.Нарисуем проекцию
Решение.Нарисуем проекцию 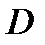 области
области 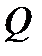 на плоскость
на плоскость  Границу
Границу 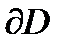 образуют прямые
образуют прямые 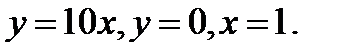 Сначала расставим пределы по
Сначала расставим пределы по 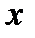 и
и  используя область
используя область 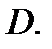 Затем возьмем произвольно точку
Затем возьмем произвольно точку  и проведем через неё луч в направлении оси
и проведем через неё луч в направлении оси  Она пересечет нижнюю границу области
Она пересечет нижнюю границу области 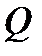 в точке
в точке 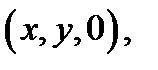 а верхнюю границу этой области – в точке
а верхнюю границу этой области – в точке 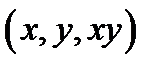 . Значит, нижний предел интеграла по
. Значит, нижний предел интеграла по 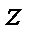 будет
будет 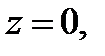 а верхний предел по
а верхний предел по 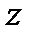 будет
будет  В результате получим
В результате получим
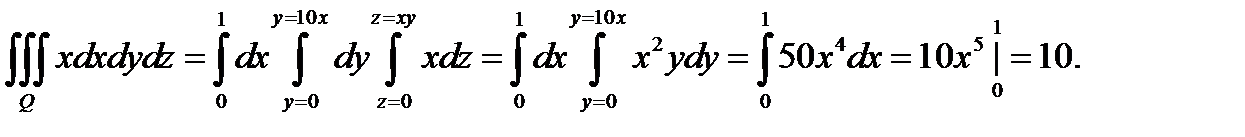
Дата добавления: 2017-03-29; просмотров: 1110;
