Неявная функция и её дифференцирование
Рассмотрим уравнение 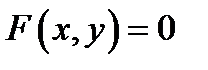 в области
в области 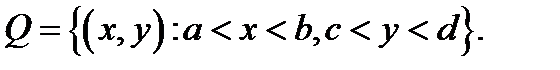
Определение 1.Говорят, что уравнение 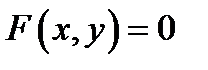 задаёт в области
задаёт в области 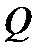 функцию
функцию 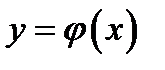 неявно, если для каждого фиксированного
неявно, если для каждого фиксированного 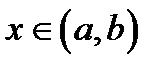 уравнение
уравнение 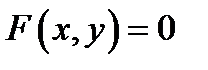 имеет единственное решение
имеет единственное решение 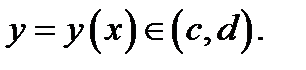 Тогда функция
Тогда функция 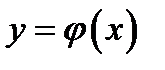 каждому
каждому  ставит в соответствие решение
ставит в соответствие решение 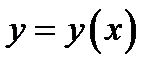 этого уравнения (т.е.
этого уравнения (т.е. 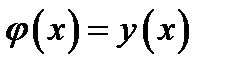 ).
).
Ясно, что если неявная функция 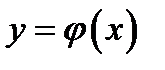 существует, то имеет место тождество
существует, то имеет место тождество 
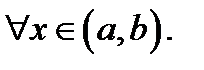 При этом часто в явном виде функцию
При этом часто в явном виде функцию 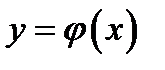 получить невозможно. Например, уравнение
получить невозможно. Например, уравнение 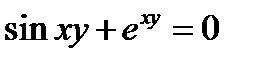 определяет в окрестности каждой фиксированной точки
определяет в окрестности каждой фиксированной точки 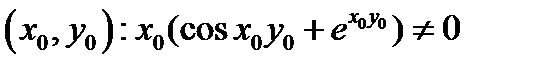 некоторую функцию
некоторую функцию 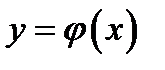 . Однако найти эту функцию в явном виде не представляется возможным.
. Однако найти эту функцию в явном виде не представляется возможным.
Обращаем также внимание на то, что неявная функция существенно связана с областью 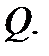 В одной из областей для одного и того же уравнения неявная функция может существовать, в другой – нет. Например, уравнение
В одной из областей для одного и того же уравнения неявная функция может существовать, в другой – нет. Например, уравнение 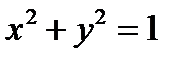 в области
в области  задаёт функцию
задаёт функцию 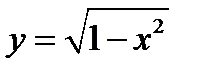 неявно, а в области
неявно, а в области  оно не задаёт никакой неявной функции
оно не задаёт никакой неявной функции 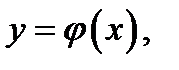 так как в этой области указанное уравнение имеет два решения
так как в этой области указанное уравнение имеет два решения 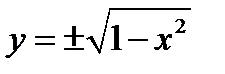 для каждого
для каждого 
Теорема 3(о существовании неявной функции). Пусть выполнены условия:
1) точка 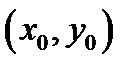 является решением уравнения
является решением уравнения 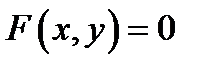 (т.е.
(т.е. 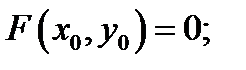 )
)
2) в некотором прямоугольнике 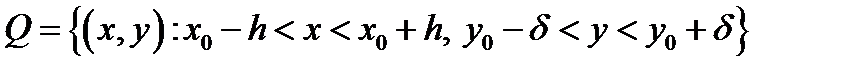 функция
функция 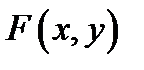 и её частные производные
и её частные производные 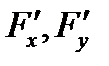 непрерывны; 3)
непрерывны; 3) 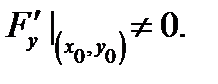
Тогда существует прямоугольник 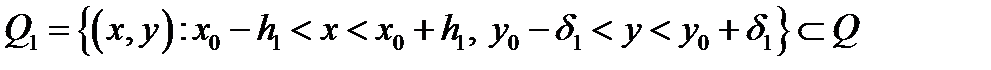 такой, что в этом прямоугольнике уравнение
такой, что в этом прямоугольнике уравнение 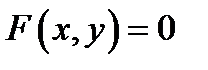 определяет некоторую функцию
определяет некоторую функцию 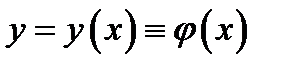 неявным образом, причём
неявным образом, причём  Кроме того, функция
Кроме того, функция 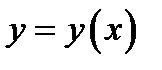 является непрерывно дифференцируемой в интервале
является непрерывно дифференцируемой в интервале 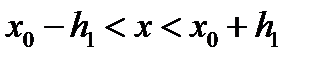 и имеет место равенство
и имеет место равенство
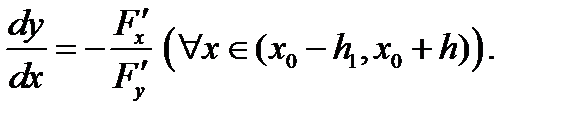
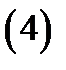
Например, указанное выше уравнение 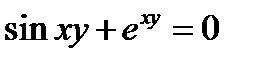 определяет в окрестности каждой фиксиро-
определяет в окрестности каждой фиксиро-
ванной точки 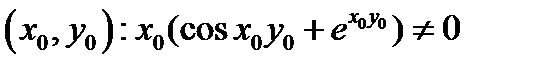 некоторую функцию
некоторую функцию 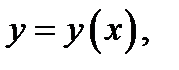 так как при таких
так как при таких
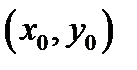 частная производная
частная производная 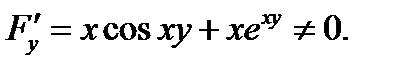 Производную этой функции вычисляем по формуле (4):
Производную этой функции вычисляем по формуле (4):  где
где 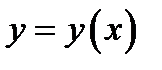 удовлетворяет уравнению
удовлетворяет уравнению 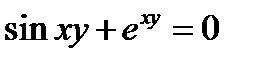 .
.
Аналогично определяются функции двух и бо̀льшего числа переменных, заданные неявно. Приведем формулировку теоремы о существовании неявной функции двух переменных.
Теорема 4.Пусть выполнены условия:
1) точка 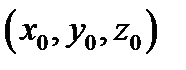 является решением уравнения
является решением уравнения  (т.е.
(т.е. 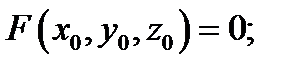 )
)
2) в некоторой области 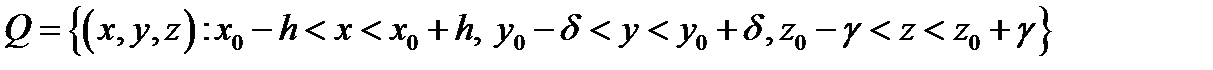 функция
функция 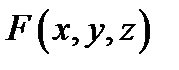 и её частные производные
и её частные производные  непрерывны; 3)
непрерывны; 3) 
Тогда существует область
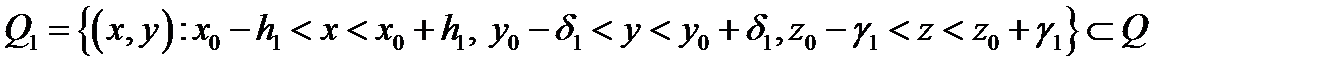
такая, что в этой области уравнение 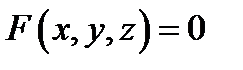 определяет некоторую функцию
определяет некоторую функцию 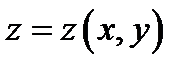 неявным образом, причём
неявным образом, причём 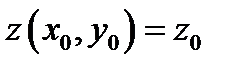 Кроме того, функция
Кроме того, функция  имеет в прямоугольнике
имеет в прямоугольнике 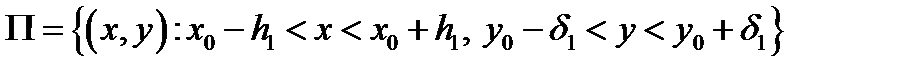 непрерывные частные производные, которые вычисляются по формулам
непрерывные частные производные, которые вычисляются по формулам
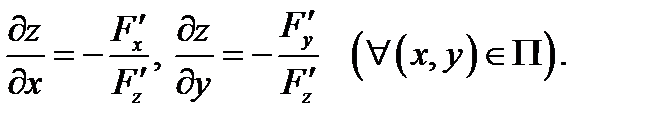

Например, для функции 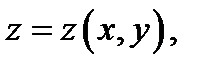 заданной неявно уравнением
заданной неявно уравнением  по формулам (5) находим
по формулам (5) находим
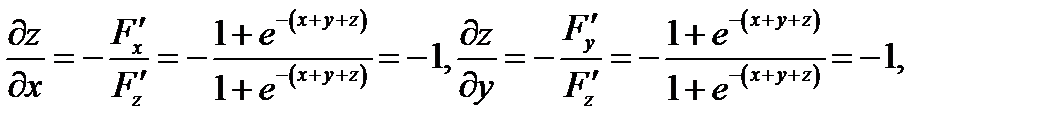
где 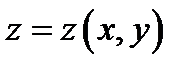 удовлетворяет уравнению
удовлетворяет уравнению 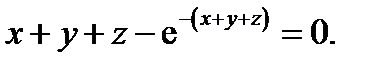
Дата добавления: 2017-03-29; просмотров: 804;
