Метрические пространства. Открытые и замкнутые множества. Понятие области

В предыдущих лекциях вводилось понятие евклидова пространства, т.е. пространства 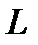со скалярным произведением 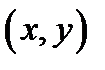( 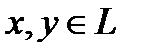). Введем теперь в рассмотрение понятие метрического пространства.

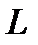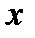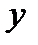Определение 1.Линейное пространство называется метрическим пространством, если в нем для любых векторов и определено число 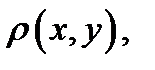называемое расстоянием между 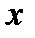и 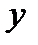(или метрикой в 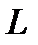), обладающее следующими свойствами:

1. П.О.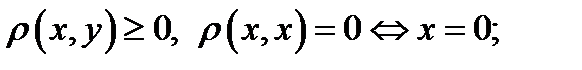

2. С.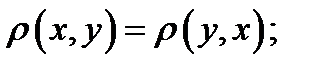

3. Т. 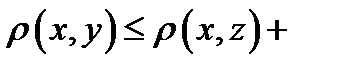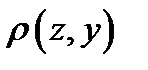( 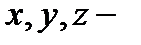произвольные векторы из пространства ).

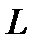Любое евклидово пространство 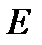является одновременно и метрическим пространст-

вом с метрикой 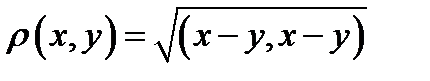(проверьте выполнение свойств 1-3). Заметим, что число 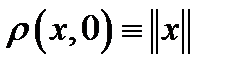называется длиной (или нормой) вектора 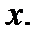Так что 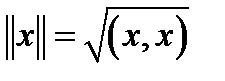в евкли-

довом пространстве 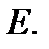Например, в 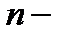мерном точечном евклидовом пространстве 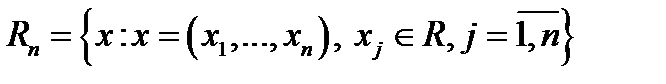метрика вводится следующим образом:

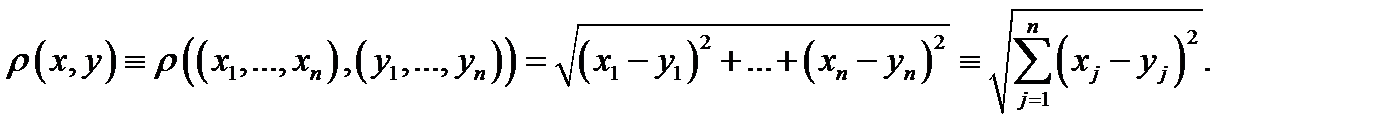
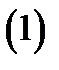
В любом метрическом пространстве 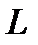можно ввести понятие окрестности точки. Если

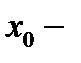фиксированная точка метрического пространства 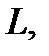то множество

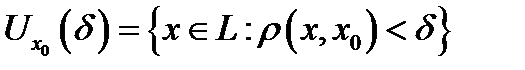
называется 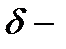окрестностью точки 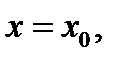а множество –

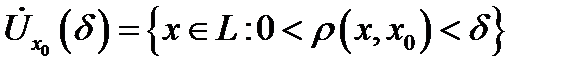проколотой 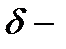окрестностью этой точки.

Мы будем работать в основном с евклидовыми пространствам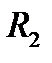и и 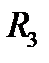, поэтому дадим описание в них окрестности точки (см. (1)):

в пространстве 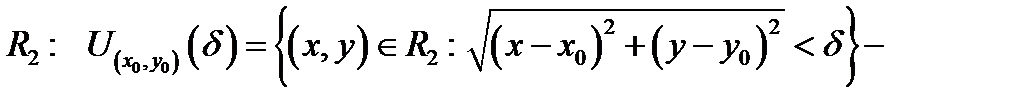открытый круг радиуса (см. Р.1);

в пространстве 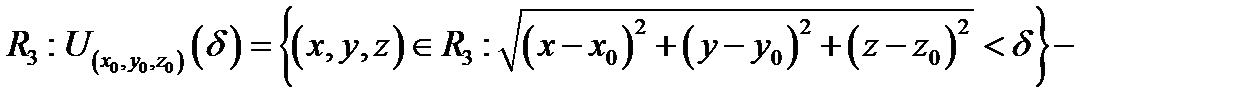откры-

тый шар радиуса

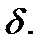
Введем теперь понятие внутренней и граничной точки множества 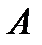метрического пространств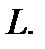а Точка 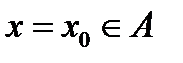называется внутренней точкой множества 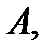если она входит в 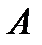вместе с некоторой своей окрестностью. Точка 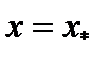называется граничной точкой множества 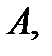если в любой окрестности этой точки существуют точки, как принадлежащие 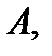так и не принадлежащие 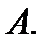Множество всех граничных точек множества 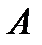образуют границу 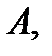которая обозначается символом 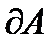или 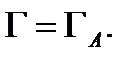Можество 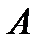называется открытым множеством, если все его точки внутренние. Если множеству 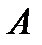принадлежат все его граничные точки, то оно называется замкнутым множеством. Точка 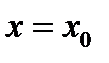называется предельной точкой множества 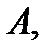если в любой окрестности этой точки существует точка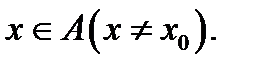

Теперь введем понятие области. При этом везде ниже рассматривается только евклидово пространство 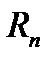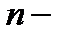мерных упорядочных точек 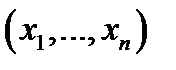с метрикой (1). Заметим сначала, что множество 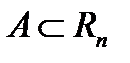называется связным, если любые две его точки можно соединить непрерывной кривой, не выходящей из 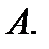И наконец, любое связное открытое множество в 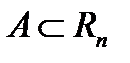называется областью.